练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    下列条件中不能使两个直角三角形全等的是（　　）

    A. 两条直角边对应相等 B. 两个锐角对应相等

    C. 一条直角边和斜边对应相等 D. 一个锐角和斜边对应相等

    B 【解析】选项A，可以利用边角边判定两三角形全等；选项B，全等三角形的判定必须有边的参与，三个角对应相等不能判定两三角形全等；选项C，根据斜边直角边定理判定两三角形全等；选项D，可以利用角角边判定两三角形全等．故选B．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2018年春人教版八年级数学下册（广西）期末测试 题型：单选题

    已知直角三角形的两直角边长分别为5和12，则此直角三角形斜边上的中线长为（）

    A. 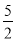B. 6 C. 13 D.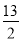

    D 【解析】已知直角三角形的两直角边长分别为5和12，根据勾股定理求得斜边为13，根据直角三角形斜边上的中线等于斜边的一半，得此直角三角形斜边上的中线长为，故选D.

    查看答案和解析>>

    科目：初中数学 来源：2017年广西南宁八中中考数学五模试卷 题型：填空题

    如图，AB是⊙O的直径，C、D为圆O上的两点，若∠CDB=35°，则∠ABC的度数为_____度．

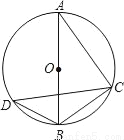
    55 【解析】由于AB是⊙O的直径，由圆周角定理可知∠ACB=90°，则∠A+∠ABC=90°，欲求∠ABC需先求出∠A的度数，已知了同弧所对的圆周角∠CDB的度数，则∠A=∠CDB=35°，由此得∠ABC=90°-∠A=55°． 故答案为：55.

    查看答案和解析>>

    科目：初中数学 来源：山西省2017-2018学年八年级上期末模拟数学试卷 题型：解答题

    如图，AB=AC，BD=DC，DF⊥AB，DE⊥AC，垂足分别是F，E．求证：DE=DF．

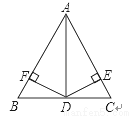
    证明见解析. 【解析】试题分析：要证DE=DF，只需证△BDF≌△CDE，已知AB=AC，可得∠B=∠C，又已知BD=DC，∠BFD=∠CED=90°，则两三角形全等可证． 试题解析：∵AB=AC，∴∠B=∠C， ∵DE⊥AB，DF⊥AC，∴∠BFD=∠CED=90°， ∵BD=DC，∴△BDF≌△CDE， ∴DE=DF．

    查看答案和解析>>

    科目：初中数学 来源：山西省2017-2018学年八年级上期末模拟数学试卷 题型：填空题

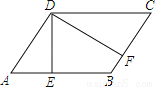
    如图，若?ABCD的周长为36cm，过点D分别作AB，BC边上的高DE，DF，且DE=4cm，DF=5cm，?ABCD的面积为 cm2．

    40 【解析】 试题分析：由?ABCD的周长为36cm，可得AB+BC=18cm①，又由过点D分别作AB，BC边上的高DE，DF，且DE=4cm，DF=5cm，由等积法，可得4AB=5BC②，继而求得答案． 【解析】 ∵?ABCD的周长为36cm， ∴AB+BC=18cm①， ∵过点D分别作AB，BC边上的高DE，DF，且DE=4cm，DF=5cm， ∴4AB...

    查看答案和解析>>

    科目：初中数学 来源：山西省2017-2018学年八年级上期末模拟数学试卷 题型：单选题

    下列各组数中能够作为直角三角形的三边长的是（　　）

    A. 1，2，3 B. 2，3，4 C. 3，4，5 D. 4，5，6

    C 【解析】【解析】 A、12+22≠32，根据勾股定理的逆定理不是直角三角形，故错误； B、22+32≠42，根据勾股定理的逆定理是直角三角形，故错误； C、32+42=52，根据勾股定理的逆定理不是直角三角形，故正确； D、42+52≠62，根据勾股定理的逆定理不是直角三角形，故错误． 故选C． 本题利用了勾股定理的逆定理判定直角三角形．

    查看答案和解析>>

    科目：初中数学 来源：2016-2017学年黑龙江省哈尔滨市松北区2017届九年级上学期期末数学试卷 题型：解答题

    已知，AB、AC是圆O的两条弦，AB=AC，过圆心O作OH⊥AC于点H．

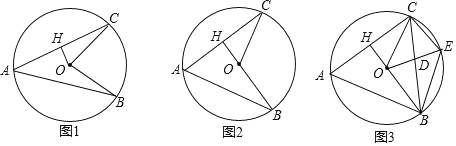
    （1）如图1，求证：∠B=∠C；

    （2）如图2，当H、O、B三点在一条直线上时，求∠BAC的度数；

    （3）如图3，在（2）的条件下，点E为劣弧BC上一点，CE=6，CH=7，连接BC、OE交于点D，求BE的长和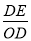的值．

    （1）证明见解析．（2）∠BAC=60°； （3）BM=5，=. 【解析】 试题分析：（1）如图1中，连接OA．欲证明∠B=∠C，只要证明△AOC≌△AOB即可． （2）由OH⊥AC，推出AH=CH，由H、O、B在一条直线上，推出BH垂直平分AC，推出AB=BC，由AB=AC，推出AB=AC=BC，推出△ABC为等边三角形，即可解决问题． （3）过点B作BM⊥CE延长...

    查看答案和解析>>

    科目：初中数学 来源：2016-2017学年黑龙江省哈尔滨市松北区2017届九年级上学期期末数学试卷 题型：单选题

    如图，DE∥BC,分别交△ABC的边AB、AC于点D、E, 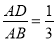, 若AE＝1，则EC=( )．

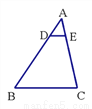
    A. 2 B. 3 C. 4 D. 6

    A 【解析】∵DE∥BC， ∴ ， ∵AE＝1， ∴AC=3 ∴EC=AC-AE=3-1=2． 故选A．

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年第一学期期末复习备考之精准复习模拟题九年级人教版数学试卷（C卷） 题型：填空题

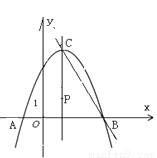
    如图，已知抛物线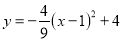，与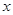轴交于A、B两点，点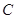为抛物线的顶点．点P在抛物线的对称轴上，设⊙P的半径为r，当⊙P与x轴和直线BC都相切时，则圆心P的坐标为___________ ．

    （1， ）或（1，-6） 【解析】设P点坐标为(1,a)， ∵抛物线的解析式为y=? (x?1)2+4， ∴抛物线顶点C的坐标为(1,4)， 令y=0,解得B点的坐标为(4,0)， 设直线BC的解析式为y=kx+b， ， 解得 ， 则直线BC的解析式为y=?x+， 点P到直线BC的距离 ， 点P到x轴的距离为|a|， 又知P与x轴和...

    查看答案和解析>>

    同步练习册答案