
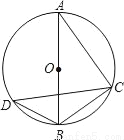
如图,AB是⊙O的直径,C、D为圆O上的两点,若∠CDB=35°,则∠ABC的度数为_____度.
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案科目:初中数学 来源:山东省德州市2017-2018学年九年级上学期期中考试数学试卷 题型:单选题
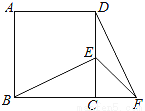
如图,在正方形ABCD中,E为DC边上的点,连接BE,将△BCE绕点C顺时针方向旋转90°得到△DCF,连接EF,若∠BEC=60°,则∠EFD的度数为_____度.
查看答案和解析>>
科目:初中数学 来源:江西省2017-2018学年度八年级第三次月考数学试卷 题型:解答题
解下列关于x的不等式(组):
(1) 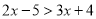 (2)
(2)
(3)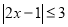 (4)
(4) 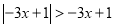
查看答案和解析>>
科目:初中数学 来源:江西省2017-2018学年度八年级第三次月考数学试卷 题型:单选题
△ABC中,AB=AC,BC=10,AB的垂直平分线与AC的垂直平分线分别交BC于点D、E且DE=4,则AD+AE的值为( )
A. 6 B. 10 C. 6或14 D. 6或10
C 【解析】分两种情况: ①如图, ∵D在AB垂直平分线上,E在AC垂直平分线上, ∴BD=AD,CE=AE, ∵BC=10,DE=4, ∴BD+CE=10-4=6, ∴AD+AE=6, ②如图, ∵D在AB垂直平分线上,E在AC垂直平分线上, ∴BD=AD,CE=AE, ∵BC=10,DE=4, ∴BD+CE=BC+DE=1...查看答案和解析>>
科目:初中数学 来源:2017年广西南宁八中中考数学五模试卷 题型:解答题
计算:(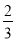 )﹣1+(π﹣3.14)0﹣2sin60°﹣
)﹣1+(π﹣3.14)0﹣2sin60°﹣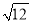 +|1﹣3
+|1﹣3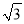 |
|
查看答案和解析>>
科目:初中数学 来源:2017年广西南宁八中中考数学五模试卷 题型:单选题
若关于x的一元二次方程kx2﹣2x﹣1=0有两个不相等的实数根,则实数k的取值范围是( )
A. k>﹣1 B. k<1且k≠0 C. k≥﹣1且k≠0 D. k>﹣1且k≠0
D 【解析】试题分析:根据一元二次方程的定义和△的意义得到k≠0且△>0,即(﹣2)2﹣4×k×(﹣1)>0,然后解不等式即可得到k的取值范围k>﹣1且k≠0. 故选D.查看答案和解析>>
科目:初中数学 来源:2017年广西南宁八中中考数学五模试卷 题型:单选题
某红外线遥控器发出的红外线波长为0.000 00094m,用科学计数法表示这个数是( )
A. 9.4×10-7m B. 9.4×107m C. 9.4×10-8m D. 9.4×108m
A 【解析】试题分析:科学计数法是指:a×,且1≤<10,小数点向右移动几位,则n的相反数就是几.查看答案和解析>>
科目:初中数学 来源:山西省2017-2018学年八年级上期末模拟数学试卷 题型:单选题
下列条件中不能使两个直角三角形全等的是( )
A. 两条直角边对应相等 B. 两个锐角对应相等
C. 一条直角边和斜边对应相等 D. 一个锐角和斜边对应相等
B 【解析】选项A,可以利用边角边判定两三角形全等;选项B,全等三角形的判定必须有边的参与,三个角对应相等不能判定两三角形全等;选项C,根据斜边直角边定理判定两三角形全等;选项D,可以利用角角边判定两三角形全等.故选B.查看答案和解析>>
科目:初中数学 来源:黑龙江省密山市2017-2018学年八年级上学期期中考试数学试卷 题型:解答题
先化简,再求值: 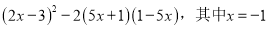 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com