
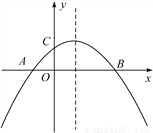
��ͼ�����κ���y��ax2��bx��c(a��0)��ͼ����x�ύ��A��B���㣬��y�ύ�ڵ�C����OA��OC.�����н��ۣ���abc��0����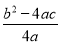 ��0����ac��b��1��0����OA��OB����
��0����ac��b��1��0����OA��OB����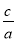 .���н�����ȷ����____________
.���н�����ȷ����____________
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2016-2017ѧ�����ɹ�ͨ���а��꼶���£���ĩ��ѧ�Ծ� ���ͣ������
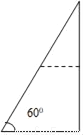
��ͼ��ʾ����һ��һ����Ϊ60���ֱ��������ֽƬ������һ����λ��������ƴ�ɵ��ı������� ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�����ɹŰ�������2017-2018ѧ����꼶���ϣ�������ѧ�Ծ� ���ͣ������
��ͼ����Rt��ABC�У���ACB=90�㣬��B=30�㣬����ABC�Ƶ�C��˳ʱ�뷽����תn�Ⱥõ���DEC����D�պ�����AB���ϣ�
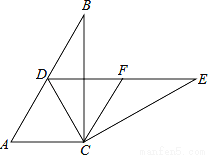
��1����n��ֵ��
��2����F��DE���е㣬�ж��ı���ACFD����״����˵�����ɣ�
(1)60����2���ı���ACFD�����Σ����ɼ�����. �����������������(1)��������ת�����ʵó�AC=CD�������ó���ADC�ǵȱ������Σ����ɵó���ACD�Ķ����� (2)������ֱ�������ε����ʵó�FC=DF�������ó�AD=AC=FC=DF�����ɵó��𰸣� ���������(1)������Rt��ABC�У���ACB=90�㣬��B=30�㣬����ABC�Ƶ�C��˳ʱ�뷽����תn�Ⱥõ���DEC��...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�����ɹŰ�������2017-2018ѧ����꼶���ϣ�������ѧ�Ծ� ���ͣ���ѡ��
������x��һԪ���η��̷��̣�k��1��x2+4x+1=0��ʵ��������k��ȡֵ��Χ�ǣ�������
A. k��5 B. k��5����k��1 C. k��5����k��1 D. k��5
C ������������������߹���x��һԪ���η��̷�����ʵ������ �� ��ã� ��k��1. ��ѡC.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ��ƽ��2018����꼶��ѧ�ڵڶ����¿���ѧ�Ծ� ���ͣ������
����ij���ճ������һ��ɱ�Ϊ10Ԫ/���Ĺ���ƷͶ���г�����������ÿ����������y���������۵���x��Ԫ/�����ĺ�����ϵʽ��y=��10x+700
��1�������۵��۶�Ϊ����ʱ�������ù���Ʒÿ���õ����������������Ƕ��٣�
��2������۲��Ź涨���ù���Ʒ���۵�����߲��ܳ���35Ԫ/������ô���۵��۶�Ϊ����ʱ�����ճ������ù���Ʒÿ���õ����������������Ƕ��٣�
��1�����۵��۶�Ϊ40Ԫ/��ʱ����������������Ϊÿ��9000Ԫ����2�������۵��۶�Ϊ35Ԫ/��ʱ��ÿ��������������������Ϊÿ��8750Ԫ. ����������������� ��1����ÿ���õ�����Ϊw������������=������Ʒ�������Ʒ�������ɵã�w=(x-10)(-10x+700)���������䷽������õ�xΪ����ʱ��w�����ֵ�����ֵ�Ƕ��٣� ��2�����ƣ�1���������䷽���w��x��ĺ�����...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ��ƽ��2018����꼶��ѧ�ڵڶ����¿���ѧ�Ծ� ���ͣ������
�㣨0��1������ԭ��O�ԳƵĵ���____________��
(0,-1) ���������㣨0��1������ԭ��ĶԳƵ�������ǣ�0��-1��. �ʴ�Ϊ����0��-1��.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ��ƽ��2018����꼶��ѧ�ڵڶ����¿���ѧ�Ծ� ���ͣ���ѡ��
������x��һԪ���η���ax2+2x��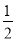 =0��a��0������������ȵ�ʵ��������a��ȡֵ��Χ�ǣ�������
=0��a��0������������ȵ�ʵ��������a��ȡֵ��Χ�ǣ�������
A. A����2 B. a����2 C. ��2��a��0 D. ��2��a��0
C ���������߹��ڵ�һԪ���η�������������ȵ�ʵ������ ���=��������ã� �� �֡ߣ� ���ȡֵ��Χ�ǣ� . ��ѡC.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ͭ��ΰ��ѧУ2017-2018ѧ����꼶��ѧ�����п�����ѧ�Ծ� ���ͣ������
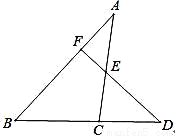
��ͼ����֪DΪ��ABC�ı�BC�ӳ�����һ�㣬DF��AB��F��AC��E����A=35�㣬��D=42�㣮
��1�����B�Ķ�����
��2�����ACD�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㽭ʡ������۴����2017-2018ѧ����꼶�ϲ���ѧ��һ���¿��Ծ� ���ͣ���ѡ��
��֪����1��y1��������2��y2��������4��y3����������y=��2x2��8x+m�ϵĵ㣬�� ��
A. y1��y2��y3 B. y3��y2��y1 C. y3��y1��y2 D. y2��y3��y1
C �������������������������ߵĶԳ��ᣬ��Ͽ��ڷ�����ͼ�����ݶԳ��Խ�����⣮ ������y=��2x2��8x+m�ĶԳ���Ϊx=��2���ҿ������£�x=��2ʱȡ�����ֵ�� �ߩ�4����1���ҩ�4����2�ľ�����ک�1����2�ľ��룬���ݶ��κ����ĶԳ��ԣ�y3��y1�� ��y3��y1��y2���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com