
二次函数y=ax2+bx+c的图象如图,点C在y轴的正半轴上,且OA=OC,则
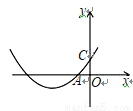
A. ac+1=b B. ab+1=c C. bc+1=a D. 以上都不是
A 【解析】试题分析:根据图象易得C(0,c)且c>0,再利用OA=OC可得A(﹣c,0),然后把A(﹣c,0)代入y=ax2+bx+c即可得到a、b、c的关系式ac+1=b. 故选A.科目:初中数学 来源:湖北省大冶市金湖街办2017-2018学年八年级上学期第二次月考(12月)数学试卷 题型:单选题
如图,点E,F在AC上,AD=BC,DF=BE,要使△ADF≌△CBE,还需要添加的一个条件是( )
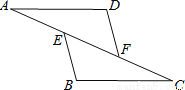
A. ∠A=∠C B. ∠D=∠B C. AD∥BC D. DF∥BE
B 【解析】试题分析:利用全等三角形的判定与性质进而得出当∠D=∠B时,△ADF≌△CBE. 当∠D=∠B时, 在△ADF和△CBE中 ∵, ∴△ADF≌△CBE(SAS)查看答案和解析>>
科目:初中数学 来源:浙江省湖州市吴兴区2017-2018学年九年级上学期期末考试数学试卷 题型:单选题
如图,已知抛物线y=x2+3x-4,把此抛物线沿y轴向上平移,平移后的抛物线和原抛物线与经过点(-2,0),(2,0)且平行于y轴的两条直线所围成的阴影部分的面积为s,平移的距离为m,则下列图象中,能表示s与m的函数关系的图象大致是( )
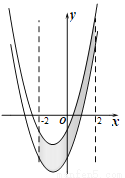
A. 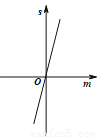 B.
B. 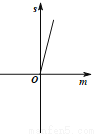 C.
C. 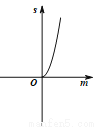 D.
D. 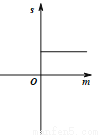
查看答案和解析>>
科目:初中数学 来源:2018春季学北师大版九年级数学下册期末测评试卷 题型:填空题
如图,☉O的直径AB=8,AC=3CB,过点C作AB的垂线交☉O于M,N两点,连接MB,则∠MBA的余弦值为_____.
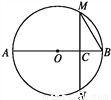
查看答案和解析>>
科目:初中数学 来源:2018春季学北师大版九年级数学下册期末测评试卷 题型:单选题
在等腰直角三角形ABC中,AB=AC=4,点O为BC的中点,以O为圆心作⊙O交BC于点M、N,⊙O与AB、AC相切,切点分别为D、E,则⊙O的半径和∠MND的度数分别为( )
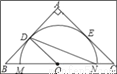
A. 2,22.5° B. 3,30° C. 3,22.5° D. 2,30°
A 【解析】试题分析:【解析】 连接OA, ∵AB与⊙O相切, ∴OD⊥AB, ∵在等腰直角三角形ABC中,AB=AC=4,O为BC的中点, ∴AO⊥BC, ∴OD∥AC, ∵O为BC的中点, ∴OD=AC=2; ∵∠DOB=45°, ∴∠MND=∠DOB=22.5°, 故选A.查看答案和解析>>
科目:初中数学 来源:宁夏2017-2018学年度上期七年级数学期末综合检测模拟试卷 题型:解答题
甲、乙两件服装的成本共500元,商店老板为获取利润,决定将甲服装按50%的利润定价,乙服装按40%的利润定价.在实际出售时,应顾客要求,两件服装均按9折出售,这样商店共获利157元,求甲、乙两件服装的成本各是多少元.
甲服装的成本为300元,乙服装的成本为200元. 【解析】试题分析:若设甲服装的成本为x元,则乙服装的成本为(500﹣x)元.根据公式:总利润=总售价﹣总进价,即可列出方程. 【解析】 设甲服装的成本为x元,则乙服装的成本为(500﹣x)元, 根据题意得:90%•(1+50%)x+90%•(1+40%)(500﹣x)﹣500=157, 解得:x=300,500﹣x=200...查看答案和解析>>
科目:初中数学 来源:宁夏2017-2018学年度上期七年级数学期末综合检测模拟试卷 题型:填空题
一个几何体由若干大小相同的小立方块搭成,如图所示的分别是从它的正面、左面看到的图形,则搭成该几何体最多需要__个小立方块.
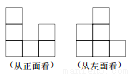
查看答案和解析>>
科目:初中数学 来源:吉林省2018届九年级(上)期中数学试卷 题型:解答题
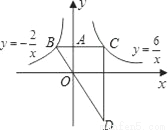
如图,在平面直角坐标系中,A为y轴正半轴上一点,过点A作x轴的平行线,交函数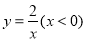 的图象于B点,交函数
的图象于B点,交函数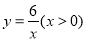 的图象于C,过C作y轴和平行线交BO的延长线于D.
的图象于C,过C作y轴和平行线交BO的延长线于D.
(1)如果点A的坐标为(0,2),求线段AB与线段CA的长度之比;
(2)如果点A的坐标为(0,a),求线段AB与线段CA的长度之比;
(3)在(1)条件下,四边形AODC的面积为多少?
查看答案和解析>>
科目:初中数学 来源:2017年四川省数学七年级(上)期末数学试卷 题型:单选题
如图所示,它需再添一个面,折叠后才能围成一个正方体,下图中的黑色小正方形分别由四位同学补画,其中正确的是( )

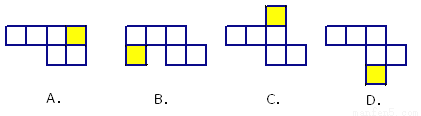
A. (A) B. (B) C. (C) D. (D)
C 【解析】试题解析:四个方格形成的“田”字的,不能组成正方体,A错; 出现“U”字的,不能组成正方体,B错; 以横行上的方格从上往下看:C选项组成正方体. 故选C.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com