
下列命题中,真命题的是( )
A. 内错角相等 B. 等腰三角形一定是等边三角形
C. 两边以及一个角对应相等的两个三角形全等 D. 全等三角形的对应边相等
D 【解析】A选项,因为只有当两直线平行时,形成的内错角才相等,而任意的两个内错角不一定相等,所以A中命题是假命题; B选项,因为等腰三角形不一定是等边三角形,所以B中命题是假命题; C选项,因为两边及一个角对应相等的两个三角形不一定全等,所以C中命题是假命题; D选项,因为全等三角形的对应边、对应角都相等,所以D中命题是真命题; 故选D.科目:初中数学 来源:福建省2017-2018学年九年级数学上学期期末检测试卷 题型:解答题
如图,已知反比例函数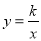 的图象与一次函数
的图象与一次函数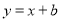 的图象交于点A(1,4)、点B(-4,n).
的图象交于点A(1,4)、点B(-4,n).
(1)求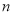 和
和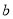 的值;
的值;
(2)求△OAB的面积;
(3)直接写出一次函数值大于反比例函数值的自变量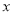 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源:湖北省武汉市青山区2017-2018学年七年级(上)期中数学试卷 题型:单选题
下列各式中,去括号正确的是( )
A. 2a2﹣(a﹣b+3c)=2a2﹣a﹣b+3c B. a+(﹣3x+y﹣2)=a﹣3x+y﹣2
C. 3x﹣[x﹣(2x﹣4)]=3x﹣x﹣2x+4 D. ﹣(x﹣y)+2(a﹣1)=﹣x+y+2a﹣1
B 【解析】试题解析:A、2a2﹣(a﹣b+3c)=2a2﹣a+b﹣3c,故本选项错误; B、a+(﹣3x+y﹣2)=a﹣3x+y﹣2,故本选项正确; C、3x﹣[x﹣(2x﹣4)]=3x﹣x+2x﹣4,故本选项错误; D、﹣(x﹣y)+2(a﹣1)=﹣x+y+2a﹣2,故本选项错误. 故选B.查看答案和解析>>
科目:初中数学 来源:浙江省2017-2018学年八年级上学期第二次学情检测数学试卷 题型:填空题
点P(2-a,a+1)在y轴上,则a=________.
2 【解析】∵点P(2-a,a+1)在y轴上, ∴,解得: . 故答案为: .查看答案和解析>>
科目:初中数学 来源:浙江省2017-2018学年八年级上学期第二次学情检测数学试卷 题型:单选题
我国纸伞的制作工艺十分巧妙,如图,伞不管是张开还是收拢,其中AE=AF,DE=DF,则△AED≌△AFD的依据是( )
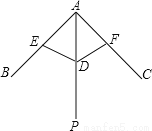
A. SAS B. ASA C. AAS D. SSS
D 【解析】∵AE=AF,DE=DF,AD是△AED和△AFD的公共边, ∴△AED≌△AFD(SSS). 故选D.查看答案和解析>>
科目:初中数学 来源:江苏省南通市2018届九年级上学期第三次月考数学试卷 题型:解答题
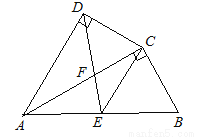
如图四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点.
(1) 求证:AC2=AB•AD;
(2) 求证:CE∥AD;
(3) 若AD=8,AB=12,求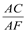 的值.
的值.
查看答案和解析>>
科目:初中数学 来源:江苏省南通市2018届九年级上学期第三次月考数学试卷 题型:解答题
计算: 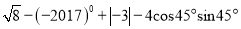
查看答案和解析>>
科目:初中数学 来源:江苏省南通市2018届九年级上学期第三次月考数学试卷 题型:单选题
cos60°的值为( )
A. 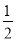 B.
B. 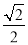 C.
C. 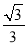 D.
D. 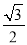
查看答案和解析>>
科目:初中数学 来源:江苏省2017-2018学年七年级12月月考数学试卷 题型:填空题
若代数式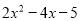 的值为7,则
的值为7,则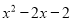 的值为 ________.
的值为 ________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com