
如图,AB是⊙O的直径,若∠BAC=35°,则∠ADC=( )
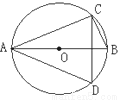
A. 35° B. 55° C. 70° D. 110°
B 【解析】试题解析:∵AB是⊙O的直径, ∴∠ACB=90°, ∵∠BAC=35°, ∴∠ABC=180°-90°-35°=55°, ∴∠ADC=∠ABC=55°. 故选B.科目:初中数学 来源:安徽省2017-2018学年度七年级第一学期人教版数学期末自测试卷(二) 题型:解答题
解方程:
(1)2x-3(2x-3)=x+4;
(2)x-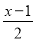 =
=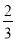 -
-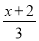 .
.
查看答案和解析>>
科目:初中数学 来源:内蒙古赤峰市宁城县2017-2018学年八年级上学期期末考试数学试卷 题型:单选题
下列从左边到右边的变形,是因式分解的是( )
A. (3-x)(3+x)=9-x2 B. x2+2x+1=x(x+1)+1
C. a2b+ab2=ab(a+b) D. (a-b)(n-m)=(b-a)(n-m)
C 【解析】因为因式分解是将多项式和的形式化成整式乘积的形式,并且分解得结果小括号外不能出现加减号,故选C.查看答案和解析>>
科目:初中数学 来源:辽宁省2018届九年级(上)期末模拟数学试卷 题型:单选题
一元二次方程4x2+1=4x的根的情况是( )
A. 只有一个实数根 B. 有两个相等的实数根 C. 有两个不相等的实数根 D. 没有实数根
B 【解析】试题解析:原方程可变形为4x2﹣4x+1=0, ∵在方程4x2﹣4x+1=0中,△=(﹣4)2﹣4×4×1=0, ∴方程4x2+1=4x有两个相等的实数根. 故选B.查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期初三数学期末试卷 题型:解答题
已知:如图,在四边形ABCD中,BD是一条对角线,∠DBC=30°,∠DBA=45°,∠C=70°.若DC=a,AB=b, 请写出求tan∠ADB的思路.(不用写出计算结果)
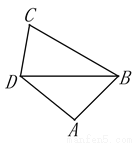
查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期初三数学期末试卷 题型:解答题
计算:4sin45°-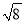 +(
+(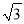 -1)0+|-2|.
-1)0+|-2|.
查看答案和解析>>
科目:初中数学 来源:江苏省南通市崇川区2015-2016学年八年级上学期期末考试数学试卷 题型:解答题
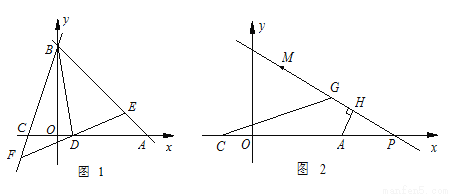
如图1,已知A(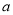 ,0),B(0,
,0),B(0, 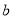 )分别为两坐标轴上的点,且
)分别为两坐标轴上的点,且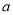 、
、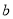 满足
满足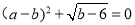 ,OC∶OA=1∶3.
,OC∶OA=1∶3.
(1)求A、B、C三点的坐标;
(2)若D(1,0),过点D的直线分别交AB、BC于E、F两点,设E、F两点的横坐标分别为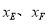 .当BD平分△BEF的面积时,求
.当BD平分△BEF的面积时,求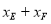 的值;
的值;
(3)如图2,若M(2,4),点P是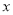 轴上A点右侧一动点,AH⊥PM于点H,在HM上取点G,使HG=HA,连接CG,当点P在点A右侧运动时,∠CGM的度数是否改变?若不变,请求其值;若改变,请说明理由.
轴上A点右侧一动点,AH⊥PM于点H,在HM上取点G,使HG=HA,连接CG,当点P在点A右侧运动时,∠CGM的度数是否改变?若不变,请求其值;若改变,请说明理由.
查看答案和解析>>
科目:初中数学 来源:北京市2017-2018学年第一学期初二数学期中试卷及答案 题型:填空题
已知, 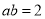 ,
, 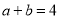 ,则式子
,则式子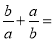 __________.
__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com