练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    在同一平面内,已知A,B,C是直线l同旁的三个点.

    (1)若AB∥l,BC∥l,那么A,B,C三点在同一条直线上吗?为什么?

    (2)若AB⊥l,BC⊥l,那么A,B,C三点在同一条直线上吗?为什么?

    （1）在；（2）在. 【解析】试题分析：（1）根据平行线的概念和公理可回答； （2）根据垂直的定义和平行公理的推论可回答. 试题解析：(1)在同一条直线上,因为直线AB,BC都经过点B,且都与直线l平行,而过直线外一点有且只有一条直线与这条直线平行,所以AB,BC为同一条直线,所以A,B,C三点在同一条直线上. (2)在同一条直线上,因为AB,BC都经过点B,且都与直线l垂...
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2017-2018学年七年级数学人教版5.1相交线同步练习 题型：单选题

    如图，直线AB，CD相交于点O，OA平分∠COE，∠COE＝70°，则∠BOD的度数是（ ）

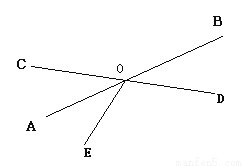
    A. 20° B. 30° C. 35° D. 40°

    C 【解析】首先利用相交线的性质确定对顶角相等，然后根据角平分线定义得出所求角与已知角的关系转化求解． 【解析】 ∵∠COE=70°且OA平分∠COE， ∴∠COA=∠COE=35°， 又∵∠COA与∠BOD是对顶角， ∴∠BOD = ∠COA =35°. 故选C.

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下册 第二章 相交线与平行线 2.2 探索直线平行的条件 同位角及平行公理 同步课堂练习题 题型：单选题

    如图，直线AB、CD被直线EF所截，则∠AMN的同位角是( )

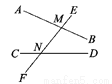
    A. ∠CNM B. ∠CNF C. ∠DNF D. ∠DNM

    B 【解析】∵直线AB、CD被直线EF所截， ∴只有∠AMN与∠CNF在截线EF的同侧，且在AB和CD的同旁， 即∠CNF是∠AMN的同位角。 故选B.

    查看答案和解析>>

    科目：初中数学 来源：人教版2017-2018学年九年级下册数学全册综合测试卷 题型：单选题

    已知α为锐角，则m=sin2α+cos2α的值（　　）

    A. m＞1                                    B. m=1                                    C. m＜1                                    D. m≥1

    B 【解析】根据同角三角函数关系，知m=sin2α+cos2α=1， 故选：B.

    查看答案和解析>>

    科目：初中数学 来源：人教版2017-2018学年九年级下册数学全册综合测试卷 题型：单选题

    下列说法正确的是（　　）

    A. 求sin30°的按键顺序是 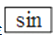、30、=

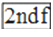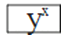    B. 求23的按键顺序 、2、 、3、=

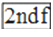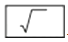    C. 求的按键顺序是、 、8、=

    D. 已知sinA=0.5018，用计算器求锐角A的大小，按键顺序是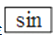、、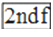0.5018、=

    A 【解析】求sin30°的按键顺序是、30、=，A正确； 求23的按键顺序2、、3、=，B错误； 求的按键顺序是、8、=，C错误； 已知sinA=0.5018,用计算器求锐角A的大小,按键顺序是先按shift键、0.5018、=，D错误， 故选：A.

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下2.2.1 用“同位角、第三直线”判定平行线 同步练习 题型：单选题

    某人在广场上练习驾驶汽车，两次拐弯后，行驶方向与原来相同，这两次拐弯的角度可能是（ ）

    A. 第一次左拐30°，第二次右拐30°

    B. 第一次右拐50°，第二次左拐130°

    C. 第一次右拐50°，第二次右拐130°

    D. 第一次向左拐50°，第二次向左拐120°

    A 【解析】试题解析：如图： 故选：A．

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下2.2.1 用“同位角、第三直线”判定平行线 同步练习 题型：单选题

    如图，直线a，b被直线c所截，下列条件能使a//b的是 ( )

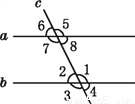
    A. ∠1=∠6 B. ∠2=∠6 C. ∠1=∠3 D. ∠5=∠7

    B 【解析】试题分析：利用平行线的判定方法判断即可．∵∠2=∠6（已知），∴a∥b（同位角相等，两直线平行）， 则能使a∥b的条件是∠2=∠6

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年九年级数学北师大版上册 全册综合测试卷1 题型：填空题

    从甲、乙2名医生和丙、丁2名护士中任意抽取2人参加医疗队，那么抽取的2人恰好是一名医生和一名护士的概率为________．

    【解析】【解析】 画树状图为： 共有12种等可能的结果数，其中恰好是一名医生和一名护士的结果数为8，所以恰好是一名医生和一名护士的概率==．故答案为： ．

    查看答案和解析>>

    科目：初中数学 来源：2018人教版九年级数学下册练习：期中检测卷 题型：解答题

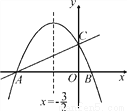
    如图，在平面直角坐标系xOy中，直线y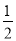＝x＋2与x轴交于点A，与y轴交于点C.抛物线y＝ax2＋bx＋c的对称轴是直线x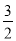＝－，且经过A，C两点，与x轴的另一交点为点B.

    (1)①直接写出点B的坐标；②求抛物线的解析式．

    (2)抛物线上是否存在点M，过点M作MN垂直x轴于点N，使得以点A，M，N为顶点的三角形与△ABC相似？若存在，求出点M的坐标；若不存在，请说明理由．

    (1)①点B的坐标为(1，0)；②y＝－x2－x＋2；(2)存在点M1(0，2)，M2(－3，2)，M3(2，－3)，M4(5，－18)，使得以点A，M，N为顶点的三角形与△ABC相似. 【解析】【试题分析】（1）①先求的直线y=x+2与x轴、y轴交点的坐标，然后利用抛物线的对称性可求得点B的坐标；②设抛物线的解析式为y=y=a（x+4）（x﹣1），然后将点C的坐标代入即可求得a的值；（3）...

    查看答案和解析>>

    同步练习册答案