
10�����б�ҵ�����п��������Գɼ����£�35 ��36 ��36 ��36 ��36�� 37 ��38�� 39�� 39�� 40 ����Щ�ɼ�����λ���ǣ� ��
A.35 B. 36 C. 36.5 D. 40
C �������� ���������10�����б�ҵ�����п��������Գɼ����£�35 ��36 ��36 ��36 ��36�� 37 ��38�� 39�� 39�� 40�������ǰ���С�������еģ��������ݵ����м������36�� 37����Щ�ɼ�����λ����36.5
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ���㽭���ݹ�����������ѧ2018����꼶��ѧ�����п�����ѧ�Ծ����������� ���ͣ���ѡ��
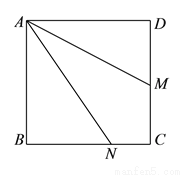
��ͼ��������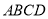 �У�
�У� 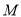 Ϊ
Ϊ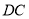 ���е㣬
���е㣬 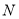 Ϊ
Ϊ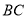 ��һ�㣬
��һ�㣬 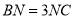 ����
����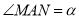 ����
����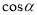 ��ֵ���ڣ� ����
��ֵ���ڣ� ����
A. 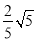 B.
B. 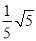 C.
C. 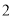 D.
D. 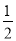
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017������ʡӪ���д�ʯ����ˮԴ���п���ѧģ���Ծ������� ���ͣ������
�Ȼ�������ֵ�� 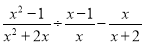 ������x���㷽��x2+4x��5=0��
������x���㷽��x2+4x��5=0��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017������ʡӪ���д�ʯ����ˮԴ���п���ѧģ���Ծ������� ���ͣ���ѡ��
����������ȷ���ǣ�������
A. x3•x3=2x3 B. a8��a4=a2 C. ����a3��2=a6 D. ��3a2b��3=9a6b3
C ��������A.x3?x3=x6���ʴ��� B.a8��a4=a4���ʴ��� C.��ȷ�� D.(3a2b)3=27a6b3���ʴ��� ��ѡ��C.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ɽ��ʡ��������ɽ�羰��2017-2018ѧ����꼶����ĩģ����ѧ�Ծ� ���ͣ������
��ͼ���ڡ�ABC�У���C=��ABC=2��A��BD��AC���ϵĸߣ����DBC�Ķ�����
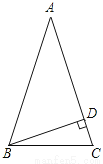
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ɽ��ʡ��������ɽ�羰��2017-2018ѧ����꼶����ĩģ����ѧ�Ծ� ���ͣ���ѡ��
����������
���������ǵ���60�㣻
����һ���ǵ���60��ĵ��������Σ�
��������ǣ�ÿ�����㴦��ȡһ����ǣ�����ȵ������Σ�
��һ���ϵ�����Ҳ���������ϵĸߵĵ��������Σ�
�����ǵȱ������ε��У�������
A. �٢ڢ� B. �٢ڢ� C. �٢� D. �٢ڢۢ�
D ��������������������ݵȱ������ε��ж��жϣ� ���������ǵ���60�㣬�������Ҳ��60�ȣ������ǵȱ������Σ�����ȷ�� ������ȱ������ε��ж�2������ȷ�� �������������������ڽ���ȣ������ǵȱ������Σ�����ȷ�� �ܸ��ݵȱ����������ߺ�һ���ʣ�����ȷ�� ���Զ���ȷ�� ��ѡD���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ɽ��ʡ��������ɽ�羰��2017-2018ѧ����꼶����ĩģ����ѧ�Ծ� ���ͣ������
��һ�����ݣ�1��3��3��4��4���������ݵķ���Ϊ________��
1.2 ���������������� �������ݵ�ƽ�����ǣ���1+3+3+4+4����5=3�� ���������ݵķ���Ϊ�� [��1��3��2+��3��3��2+��3��3��2+2����4��3��2]=1.2���ʴ�Ϊ��1.2���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017�����ʡ�˲����п���ѧģ���Ծ������� ���ͣ������
С����β��Գɼ����£�91��89��88��90��92��������β��Գɼ���ƽ������_____��������_____��
90 2 ���������������������91��89��88��90��92ƽ����Ϊ�� =90�� ����ΪS2= [��91-90��2+��89-90��2+��88-90��2+��90-90��2+��92-90��2]=2�� ����90��2���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017��ӱ�ʡ�п���ѧģ���Ծ� ���ͣ������
��ͼ��AB=AD��AC=AE����1=��2����֤��BC=DE��
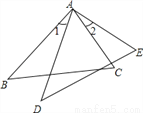
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com