
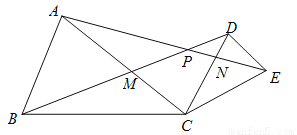
如图, 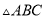 和
和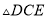 均是等腰三角形,
均是等腰三角形, 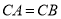 ,
, 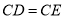 ,
, 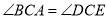 .
.
(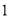 )求证:
)求证: 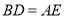 ;
;
(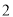 )若
)若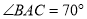 ,求
,求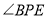 的度数.
的度数.
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:初中数学 来源:新疆乌鲁木齐市2017-2018学年七年级上学期期末考试数学试卷 题型:填空题
如图,将一副直角三角板如图放置,若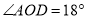 ,则
,则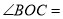 __度.
__度.
查看答案和解析>>
科目:初中数学 来源:江苏省东部分校2017-2018学年七年级上学期期末考试数学试卷 题型:解答题
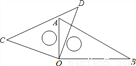
如图,直线 AB,CD 相交于点O,OE 平分∠AOD,OF⊥OC.
(1)图中∠AOF 的余角是 (把符合条件的角都填出来);
(2)如果∠AOC=130°36′,那么根据 ,可得∠BOD= °;
(3)如果∠1与∠3的度数之比为3:4,求∠EOC和∠2的度数.
查看答案和解析>>
科目:初中数学 来源:江苏省东部分校2017-2018学年七年级上学期期末考试数学试卷 题型:填空题
数轴上表示一个数的点与原点的距离是6,那么这个数是_______.
±6 【解析】【解析】 ∵|±6|=6,∴数轴上表示一个数的点与原点的距离是6,那么这个数是±6.故答案为:±6.查看答案和解析>>
科目:初中数学 来源:江苏省东部分校2017-2018学年七年级上学期期末考试数学试卷 题型:单选题
在1,-3,-1这三个数中,任意两数之和的最大值是( ).
A. 1 B. -2 C. -4 D. 0
D 【解析】【解析】 ∵-3<-1<1,∴任意两数之和的最大值是:-1+1=0.故选D.查看答案和解析>>
科目:初中数学 来源:浙江杭州富阳2016-2017学年八年级上学期期末数学试卷 题型:填空题
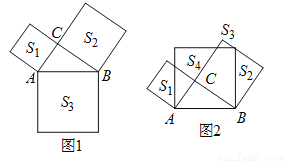
如图,在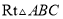 中,
中, 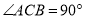 ,
, 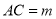 ,
, 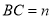 ,分别以三角形的三条边为边作正方形.
,分别以三角形的三条边为边作正方形.
(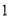 )若三个正方形的位置如图
)若三个正方形的位置如图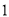 所示,其中阴影部分的面积
所示,其中阴影部分的面积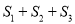 的值为__________.(结果用含
的值为__________.(结果用含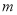 ,
, 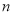 的代数式表示)
的代数式表示)
( )若三个正方形的位置如图
)若三个正方形的位置如图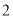 所示,其中阴影部分的面积
所示,其中阴影部分的面积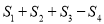 的值为__________.(结果用含
的值为__________.(结果用含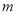 ,
,  的代数式表示)
的代数式表示)
查看答案和解析>>
科目:初中数学 来源:浙江杭州富阳2016-2017学年八年级上学期期末数学试卷 题型:单选题
科目:初中数学 来源:江苏省泰兴市2017-2018学年八年级上学期期末考试数学试卷 题型:解答题
(1)计算: 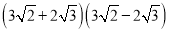 ; (2)解方程:
; (2)解方程: 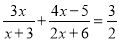 .
.
查看答案和解析>>
科目:初中数学 来源:四川省宜宾市2017-2018学年上学期期末教学质量监测八年级数学试卷 题型:解答题
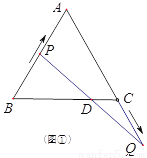
在边长为10的等边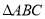 中,点
中,点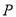 从点
从点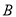 出发沿射线
出发沿射线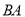 移动,同时点
移动,同时点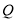 从点
从点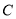 出发沿线段
出发沿线段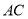 的延长线移动,点
的延长线移动,点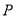 、
、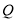 移动的速度相同,
移动的速度相同, 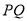 与直线
与直线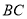 相交于点
相交于点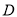 .
.
(1)如图①,当点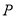 为
为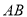 的中点时,
的中点时,
(I)求证: 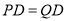 ;(II)求
;(II)求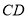 的长;
的长;
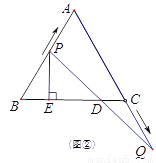
(2)如图②,过点 作直线
作直线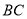 的垂线,垂足为
的垂线,垂足为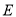 ,当点
,当点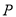 、
、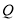 在移动的过程中,试确定
在移动的过程中,试确定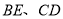 的数量关系,并说明理由.
的数量关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com