
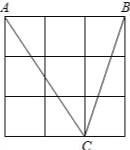
如图,方格纸中△ABC的3个顶点分别在小正方形的顶点(格点)上,这样的三角形叫格点三角形,图中与△ABC全等的格点三角形共有 个(不含△ABC).
科目:初中数学 来源:《概率的进一步认识》单元测试4 题型:解答题
某商场设立了一个可以自由转动的转盘,并做如下规定:顾客购物80元以上就获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品,下表是活动进行中的一组统计数据.

(1)计算并完成表格;
(2)请估计,当n很大时,频率将会接近多少?
(3)假如你去转动该盘一次,你获得洗衣粉的概率约是多少?
(4)在该转盘中,表示“洗衣粉”区域的扇形的圆心角约是多少?(精确到1°)
(1)0.68 0.74 0.68 0.69 0.705 0.701(2)0.7(3)0.7 (4)252° 【解析】试题分析:(1)根据频率的算法,频率=,可得各个频率;填空即可; (2)根据频率的定义,可得当n很大时,频率将会接近其概率; (3)根据概率的求法计算即可; (4)根据扇形图中,每部分占总体的百分比等于该部分所对应的扇形圆心角的度数与360°的比计算即可. ...查看答案和解析>>
科目:初中数学 来源:人教版九年级上册数学 22.1.4二次函数yax2+bx+c的图象和性质(2)测试 题型:填空题
若抛物线y=ax2+bx+c的顶点是A(2,1),且经过点B(1,0),则抛物线的函数关系式为__________________.
y = 【解析】试题分析:设抛物线的解析式为y=a(x-2)2+1,将点B(1,0)代入解析式即可求出a的值,从而得到二次函数解析式. 试题解析:设抛物线的解析式为y=a(x-2)2+1, 将B(1,0)代入y=a(x-2)2+1得, a=-1, 函数解析式为y=-(x-2)2+1, 展开得y=-x2+4x-3.查看答案和解析>>
科目:初中数学 来源:天津市 2017-2018学年 八年级数学上册 全等三角形判定 填空题练习(含答案) 题型:填空题
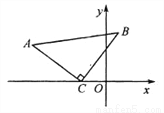
如图,在△ACB中,∠ACB=90°,AC=BC,点C的坐标为(-2,0),若点A的坐标为(-6,3),则点B的坐标是__________.
查看答案和解析>>
科目:初中数学 来源:天津市 2017-2018学年 八年级数学上册 全等三角形判定 填空题练习(含答案) 题型:填空题
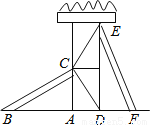
如图,有两个长度相同的滑梯(即BC=EF),左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,则∠ABC+∠DFE=___________度.
查看答案和解析>>
科目:初中数学 来源:天津市 2017-2018学年 八年级数学上册 全等三角形判定 填空题练习(含答案) 题型:填空题
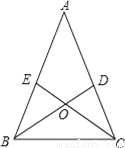
如图,在△ABC中,AB=AC,∠ABC、∠ACB的平分线BD,CE相交于O点,且BD交AC于点D,CE交AB于点E,某同学分析图形后得出以下结论,上述结论一定正确的是______(填代号).
①△BCD≌△CBE;②△BAD≌△BCD;③△BDA≌△CEA;④△BOE≌△COD;⑤△ACE≌△BCE.
查看答案和解析>>
科目:初中数学 来源:天津市 2017-2018学年 八年级数学上册 全等三角形判定 填空题练习(含答案) 题型:填空题
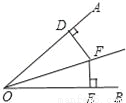
如图,FD⊥AO于D,FE⊥BO于E,下列条件:①OF是∠AOB的平分线;②DF=EF;③DO=EO;④∠OFD=∠OFE.其中能够证明△DOF≌△EOF的条件的个数有__个.
查看答案和解析>>
科目:初中数学 来源:重庆市华东师大版2016-2017学年七年级下学期期中考试数学试卷 题型:填空题
我国古代数学名著《孙子算经》中有这样一题,今有鸡兔同笼,上有35头,下有94足,问鸡兔各几何?此题的答案是:鸡有23只,兔有12只,现在小敏将此题改编为:今有鸡兔同笼,上有33头,下有88足,问鸡兔各几何?则此时的答案是:鸡有 只,兔有 只.
22,11 【解析】设鸡有x只,兔有y只,根据题意可得,解得: ,即鸡有22只,兔有11只.查看答案和解析>>
科目:初中数学 来源:北师大版(2012) 九年级上册同步练习:1.2矩形的性质 题型:单选题
矩形ABCD的长为5,宽为3,点E、F将AC三等分,则△BEF的面积为( ).
A. 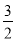 B.
B. 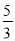 C.
C. 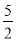 D. 5
D. 5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com