
七年级某同学做一道题:“已知两个多项式A,B, 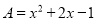 ,计算
,计算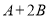 ”,他误将
”,他误将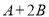 写成了
写成了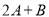 ,结果得到答案
,结果得到答案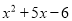 ,请你帮助他求出正确的答案.
,请你帮助他求出正确的答案.
科目:初中数学 来源:江苏省宿迁市2017-2018学年上学期第二次形成性测试七年级数学试卷 题型:填空题
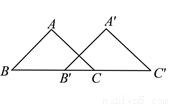
如图,将三角形ABC沿直线BC向右平移得到三角形A′B′C′,已知BC′=10,C B′=2,则BB′的长为_____.
查看答案和解析>>
科目:初中数学 来源:浙江省余姚市2017-2018学年七年级上学期期中考试数学试卷 题型:解答题
数轴是一个非常重要的数学工具,它使数和数轴上的点建立起对应关系,揭示了数与点之间的内在联系,它是“数形结合”的基础。小白在草稿纸上画了一条数轴进行操作探究:
操作一:
(1)折叠纸面,若使1表示的点与﹣1表示的点重合,则﹣2表示的点与_______表示的点重合;
操作二:
(2)折叠纸面,若使1表示的点与﹣3表示的点重合,回答以下问题:
①3表示的点与_______表示的点重合;
②若数轴上A、B两点之间距离为7(A在B的左侧),且A、B两点经折叠后重合,则A、B两点表示的数分别是______________;
操作三:
(3)在数轴上剪下9个单位长度(从﹣1到8)的一条线段,并把这条线段沿某点折叠,然后在重叠部分某处剪一刀得到三条线段(例如下图). 若这三条线段的长度之比为1:1:2,则折痕处对应的点所表示的数可能是_____________________.

查看答案和解析>>
科目:初中数学 来源:浙江省余姚市2017-2018学年七年级上学期期中考试数学试卷 题型:单选题
有一个两位数,十位数字是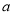 ,个位数字是
,个位数字是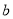 ,若把它们的位置交换,得到新的两位数是( )
,若把它们的位置交换,得到新的两位数是( )
A. 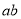 B.
B. 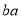 C.
C. 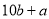 D.
D. 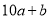
查看答案和解析>>
科目:初中数学 来源:浙江省余姚市2017-2018学年七年级上学期期中考试数学试卷 题型:单选题
计算:(-8)+(+5)=( )
A. 3 B. -3 C. 13 D. -13
B 【解析】试题解析:(-8)+(+5)=-8+5=-3 故选B.查看答案和解析>>
科目:初中数学 来源:海南省定安县2017-2018学年七年级上学期期末考试数学试卷 题型:填空题
若多项式A满足A+(2a2-b2)=3a2-2b2,则A =_________.
a2-b2 【解析】【解析】 A=3a2﹣2b2﹣(2a2﹣b2)=3a2﹣2b2﹣2a2+b2=a2﹣b2.故答案为:a2﹣b2.查看答案和解析>>
科目:初中数学 来源:海南省定安县2017-2018学年七年级上学期期末考试数学试卷 题型:单选题
如果单项式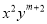 与
与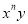 的和仍然是一个单项式,则m、n的值是( )
的和仍然是一个单项式,则m、n的值是( )
A. m=2,n=2 B. m=-1,n=2 C. m=-2,n=2 D. m=2,n=-1
B 【解析】根据单项式的和为单项式,说明这两个单项式是同类项,因此相同字母的指数相同,即n=2,m+2=1,解得m=-1. 故选:B查看答案和解析>>
科目:初中数学 来源:云南省2018届九年级上学期期中考试数学试卷 题型:解答题
解方程:(2x+3)2=2x+3
【解析】试题分析:先移项,再运用因式分解法求解即可. 试题解析:移项, 添括号, 分解因式=0, 化简(2x+3)(2x+2)=0, 即2x+3=0或2x+2=0, ∴ .查看答案和解析>>
科目:初中数学 来源:上海市长宁区2018届九年级上学期期末质量检测数学试卷 题型:解答题
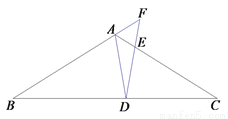
如图,在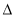 ABC中,点D在边BC上,联结AD,∠ADB=∠CDE,DE交边AC于点E,DE交BA延长线于点F,且
ABC中,点D在边BC上,联结AD,∠ADB=∠CDE,DE交边AC于点E,DE交BA延长线于点F,且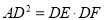 .
.
(1)求证: 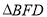 ∽
∽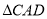 ;
;
(2)求证: 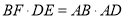 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com