
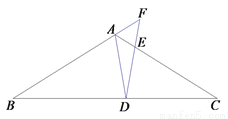
如图,在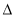 ABC中,点D在边BC上,联结AD,∠ADB=∠CDE,DE交边AC于点E,DE交BA延长线于点F,且
ABC中,点D在边BC上,联结AD,∠ADB=∠CDE,DE交边AC于点E,DE交BA延长线于点F,且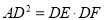 .
.
(1)求证: 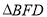 ∽
∽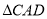 ;
;
(2)求证: 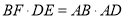 .
.
 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案科目:初中数学 来源:海南省定安县2017-2018学年七年级上学期期末考试数学试卷 题型:解答题
七年级某同学做一道题:“已知两个多项式A,B, 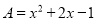 ,计算
,计算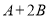 ”,他误将
”,他误将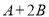 写成了
写成了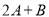 ,结果得到答案
,结果得到答案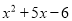 ,请你帮助他求出正确的答案.
,请你帮助他求出正确的答案.
查看答案和解析>>
科目:初中数学 来源:云南省2018届九年级上学期期中考试数学试卷 题型:填空题
已知二次函数的图象开口向下,?且顶点坐标(0,-3).请写出一个符合条件的二次函数的解析式_____________.
y=-x2-3 【解析】试题解析:∵若二次函数的图象开口向下,且经过(0,-3)点, ∴y=-x2-3符合要求. 答案不唯一.查看答案和解析>>
科目:初中数学 来源:2017-2018学年黑龙江省大庆市杜尔伯特县七年级(上)期末数学试卷(五四学制) 题型:填空题
如果收入50元,记作+50元,那么支出30元记作_____元.
-30 【解析】【解析】 如果收入50元,记作+50元,那么支出30元记作﹣30元,故答案为:﹣30.查看答案和解析>>
科目:初中数学 来源:2017-2018学年黑龙江省大庆市杜尔伯特县七年级(上)期末数学试卷(五四学制) 题型:单选题
若关于x的方程mxm-2-m+3=0是一元一次方程,则这个方程的解是( )
A. x=0 B. x=3 C. x=-3 D. x=2
A 【解析】试题分析:只含有一个未知数(元),并且未知数的指数是1(次)的方程叫做一元一次方程,它的一般形式是ax+b=0(a,b是常数且a≠0),高于一次的项系数是0. 【解析】 由一元一次方程的特点得m﹣2=1,即m=3, 则这个方程是3x=0, 解得:x=0. 故选:A.查看答案和解析>>
科目:初中数学 来源:上海市长宁区2018届九年级上学期期末质量检测数学试卷 题型:填空题
如图,在边长为2的菱形ABCD中, 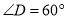 ,点E、F分别在边AB、BC上. 将
,点E、F分别在边AB、BC上. 将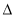 BEF沿着直线EF翻折,点B恰好与边AD的中点G重合,则BE的长等于________.
BEF沿着直线EF翻折,点B恰好与边AD的中点G重合,则BE的长等于________.
查看答案和解析>>
科目:初中数学 来源:上海市长宁区2018届九年级上学期期末质量检测数学试卷 题型:填空题
已知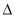 ABC与
ABC与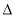 DEF相似,且
DEF相似,且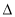 ABC与
ABC与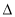 DEF的相似比为2:3,若
DEF的相似比为2:3,若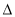 DEF 的面积为36,则
DEF 的面积为36,则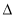 ABC的面积等于________.
ABC的面积等于________.
查看答案和解析>>
科目:初中数学 来源:北京市分校2017-2018学年度第一学期八年级数学期中试卷 题型:解答题
先化简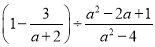 ,然后从
,然后从 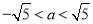 的范围内选取一个合适的整数作为a的值代入求值.
的范围内选取一个合适的整数作为a的值代入求值.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年八年级数学下册(人教版):期中检测题 题型:单选题
如图,边长为6的大正方形中有两个小正方形,若两个小正方形的面积分别为S1、S2 , 则S1+S2的值为( )
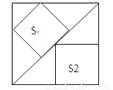
A. 16 B. 17 C. 18 D. 19
B 【解析】试题分析:由图可得,S2的边长为3,由AC=BC,BC=CE=CD,可得AC=2CD,CD=2,EC=2;然后,分别算出S1、S2的面积,即可解答. 【解析】 如图, 设正方形S1的边长为x, ∵△ABC和△CDE都为等腰直角三角形, ∴AB=BC,DE=DC,∠ABC=∠D=90°, ∴sin∠CAB=sin45°==,即AC=BC,同理可得:B...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com