
��ͼ���ڡ�ABC�У�AB=AC��AB=8��BC=12���ֱ���AB��ACΪֱ������Բ����ͼ����Ӱ���ֵ�����ǣ� ��
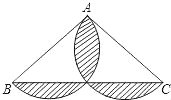
A��64��12 B��16��32
B��16��32
C��16��24 D��16��12
D��16��12
 �㽭��У��ʦ���ϵ�д�
�㽭��У��ʦ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ������ʡ�����а�����2017-2018ѧ����꼶��ѧ����ĩ������ѧ�Ծ� ���ͣ������
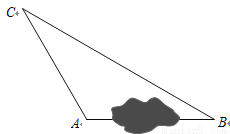
��һ�ο���ʵ����У�ͬѧ��Ҫ����ij���˹�������A��B������֮ͤ��ľ��룮�ֲ��AC��50m��BC��100m����CAB��120�㣬�����A��B������֮ͤ��ľ��룮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ��̨�е�����������2017-2018ѧ��ȵ�һѧ�ڵ����νμ�����꼶��ѧ�Ծ� ���ͣ������
��������� ��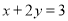 ����
����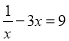 ����
����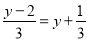 ����
����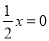 ����һԪһ�η��̵���________.����ţ�
����һԪһ�η��̵���________.����ţ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017�����ʡ�п���ѧ��ģ�Ծ� ���ͣ������
���㣺
��1�����㣺����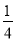 ����1��|��
����1��|��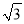 |��20110+��
|��20110+��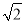 ��2+tan60�㣻
��2+tan60�㣻
��2�����ʽ���̣� 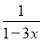 ��
��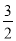 =
=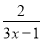 ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017�����ʡ�п���ѧ��ģ�Ծ� ���ͣ���ѡ��
����ͼ�����κ���y=ax2+bx+c��a��0����ͼ����x�ύ��A��B���㣬��y�ύ��C�㣬�ҶԳ���Ϊx=1����B����Ϊ����1��0������������ĸ����ۣ���2a+b=0����4a��2b+c��0����ac��0���ܵ�y��0ʱ��x����1��x��2��������ȷ�ĸ����ǣ� ��
A. 1 B. 2 C. 3 D. 4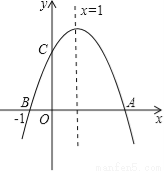
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017�����ʡ�п���ѧ��ģ�Ծ� ���ͣ���ѡ��
һ������2��5��4��3��5��4��5����λ���������ֱ��ǣ� ��.
A��3.5��5 B��4��4 C��4��5 D��4.5��4
C. �������� ���������������������λ���ĸ�����⣮�������ݰ��մ�С�����˳������Ϊ��2��3��4��4��5��5��5��������Ϊ5����λ��Ϊ4�� ��ѡ��C.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���ƽ�30��ϵ�� ���꼶��ѧ �������� ���ͣ������
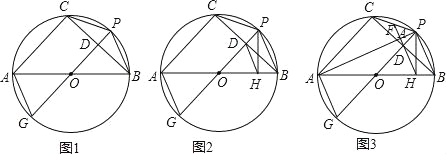
��O�ǡ�ABC�����Բ��AB��ֱ������ ���е�P����O��ֱ��PG������BC�ཻ�ڵ�D������AG��CP��PB��
���е�P����O��ֱ��PG������BC�ཻ�ڵ�D������AG��CP��PB��
��1����ͼ1����֤��AG=CP��
��2����ͼ2������P��AB�Ĵ��ߣ�����Ϊ��H������DH����֤��DH��AG��
��3����ͼ3������PA���ӳ�HD�ֱ���PA��PC�ཻ�ڵ�K��F����֪FK=2����ODH�����Ϊ2 ����AC�ij���
����AC�ij���
���𰸡���1��֤����������
��2��֤����������
��3��AC=10
��������
�����������1�����õȻ����Ե�Բ�ܽ���ȼ�����⣻
��2�����õȻ����Ե�Բ�ܽ���ȣ��õ�����ȡ�APG=��CAP���жϳ���BOD�ա�POH���ٵõ�����ȣ��Ӷ��жϳ���ƽ�У�
��3�������������ƣ��ó�����ʽ����HON�ס�CAM�� �����жϳ��ı���CDHM��ƽ���ı��Σ�������㼴����⣮
�����жϳ��ı���CDHM��ƽ���ı��Σ�������㼴����⣮
�����������1���߹�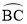 ���е�P����O��ֱ��PG��
���е�P����O��ֱ��PG��
��CP=PB��
��AB��PG���ཻ��ֱ����
��AG=PB��
��AG=CP��
��2��֤������ͼ 2������BG
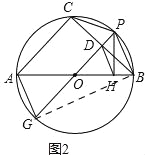
��AB��PG���ǡ�O��ֱ����
���ı���AGBP�Ǿ��Σ�
��AG��PB��AG=PB��
��P�ǻ�BC���е㣬
��PC=BC=AG��
�AG=��CP��
���APG=��CAP��
��AC��PG��
��PG��BC��
��PH��AB��
���BOD=90��=��POH��
�ڡ�BOD�͡�POH�У�
 ��
��
���BOD�ա�POH��
��OD=OH��
���ODH= ��180�㩁��BOP��=��OPB��
��180�㩁��BOP��=��OPB��
��DH��PB��AG��
��3����ͼ3����CM��AP��M��ON��DH��N��
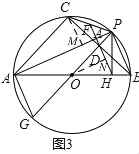
���HON= ��BOP=
��BOP= ��COP=��CAP��
��COP=��CAP��
���HON�ס�CAM��
�� ��
��
��PQ��AC��Q��
���ı���CDPQ�Ǿ��Σ�
��APH���APQ����AP�Գƣ�
��HQ��AP��
�ɣ�1���У�HK��AP��
���K��HQ�ϣ�
��CK=PK��
��PK�ǡ�CMP����λ�ߣ�
��CM=2FK=4��MF=PF��
��CM��AP��HK��AP��
��CM��HK��
���BCM+��CDH=180�㣬
�ߡ�BCM=��CAP=��BAP=��PHK=��MHK��
���MHK+��CDH=180�㣬
���ı���CDHM��ƽ���ı��Σ�
��DH=CM=4��DN=HN=2��
��S��ODH= DH��ON=
DH��ON= ��4��ON=2
��4��ON=2 ��
��
��ON= ��
��
��OH=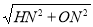 =5��
=5��
��AC= =10��
=10��
���㣺Բ���ۺ��⣮
�����͡������
��������
16
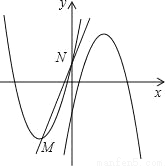
��ͼ����ƽ��ֱ������ϵ�У���֪������C1��y= �Ķ���ΪM����y���ཻ�ڵ�N���Ƚ�������C1��x�ᷭ�ۣ�������ƽ��p����λ���Ⱥ�õ�������C2��ֱ��l��y=kx+b����M��N���㣮
�Ķ���ΪM����y���ཻ�ڵ�N���Ƚ�������C1��x�ᷭ�ۣ�������ƽ��p����λ���Ⱥ�õ�������C2��ֱ��l��y=kx+b����M��N���㣮
��1�����ͼ��ֱ��д������ʽ x2+6x+2��kx+b�Ľ⼯��
x2+6x+2��kx+b�Ľ⼯��
��2����������C2�Ķ������M����ԭ��Գƣ���p��ֵ��������C2�Ľ���ʽ��
��3����ֱ��l��y������ƽ��q����λ���Ⱥ��루2���е�������C2���ڹ����㣬
��3��4q�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���ƽ�30��ϵ�� ���꼶��ѧ С������ ���ͣ������
ij��Ϊ�ᳫ��Լ��ˮ����ȡ�ֶ��շѣ���ÿ��ÿ����ˮ��������20 m3��ÿ�������շ�2Ԫ������ˮ������20 m3����������ÿ��������1Ԫ��С����5�·ݽ�ˮ��64Ԫ�������Ҹ�����ˮ________��
28 m3 �����������������64>40�����ж�С������ˮ����20����������ˮλx����40+3��x-20��=64�����x=28���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ���һѧ����ĩ��ϰ����֮����ϰģ������꼶�˽̰���ѧ�Ծ���A���� ���ͣ������
��֪���������ε�һ�ߵ���3��һ�ߵ���6����ô�����ܳ�����_______________.
15 �������������������������Ϊ3���ױ߳�Ϊ6�� ��3+3=6�� �����������Σ���ȥ�� ��������Ϊ6���ױ߳�Ϊ3�� �������ܳ��ǣ�6+6+3=15. �������ܳ���15�� �ʴ�Ϊ��15.�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com