
某市为提倡节约用水,采取分段收费.若每户每月用水量不超过20 m3,每立方米收费2元;若用水量超过20 m3,超过部分每立方米加收1元.小明家5月份交水费64元,则他家该月用水________.
28 m3 【解析】试题分析:64>40可以判定小明家用水超过20,可以设用水位x,则40+3(x-20)=64,解得x=28,科目:初中数学 来源:江苏省东台市第三教育联盟2017-2018学年度第一学期第三次阶段检测七年级数学试卷 题型:解答题
如图是由一些棱长都为1cm的小正方体组合成的简单几何体.
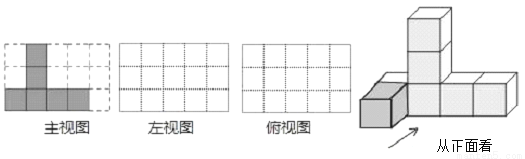
(1)该几何体的主视图如图所示,请在下面方格纸中分别画出它的左视图和俯视图;
(2)如果在这个几何体上再添加一些小正方体,并保持俯视图和左视图不变,最多可以再添加________块小正方体.
6 【解析】试题分析:(1)、根据长对正,高平齐和宽相等的法则画出三视图;(2)、根据三视图的法则得出立体图形,从而得出答案. 试题解析:【解析】 (1)如图所示: ; (2)保持俯视图和左视图不变,最多可以再添加6块小正方体.查看答案和解析>>
科目:初中数学 来源:2017年贵州省中考数学二模试卷 题型:单选题
如图,在△ABC中,AB=AC,AB=8,BC=12,分别以AB、AC为直径作半圆,则图中阴影部分的面积是( )
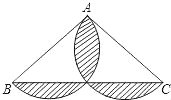
A.64π﹣12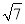 B.16π﹣32
B.16π﹣32
C.16π﹣24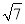 D.16π﹣12
D.16π﹣12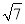
查看答案和解析>>
科目:初中数学 来源:黄金30题系列 九年级数学 大题易丢分 题型:解答题
如图1是一个三棱柱包装盒,它的底面是边长为10cm的正三角形,三个侧面都是矩形.现将宽为15cm的彩色矩形纸带AMCN裁剪成一个平行四边形ABCD(如图2),然后用这条平行四边形纸带按如图3的方式把这个三棱柱包装盒的侧面进行包贴(要求包贴时没有重叠部分),纸带在侧面缠绕三圈,正好将这个三棱柱包装盒的侧面全部包贴满.在图3中,将三棱柱沿过点A的侧棱剪开,得到如图4的侧面展开图.为了得到裁剪的角度,我们可以根据展开图拼接出符合条件的平行四边形进行研究.
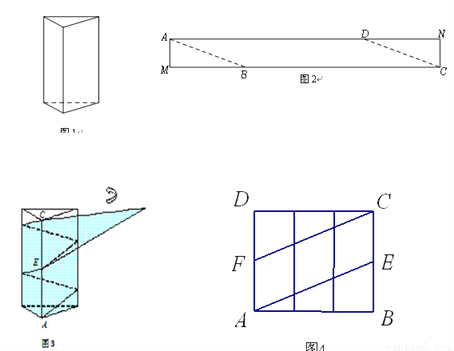
(1)请在图4中画出拼接后符合条件的平行四边形;
(2)请在图2中,计算裁剪的角度(即∠ABM的度数).
【答案】(1)作图见解析;(2)∠ABM=30°.
【解析】分析:(1)将图4中的△ABE向左平移30cm,△CDF向右平移30cm,拼成如图中的平行四边形,此平行四边形即为图2中的四边形ABCD.
(2)根据题意先求得AB=30cm,由纸带的宽为15cm,根据三角函数求得∠AMB=30°.
本题解析:(1)如图:
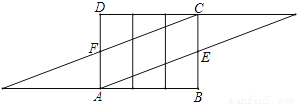
(2)由图2的包贴方法知:AB的长等于三棱柱的底边周长,∴AB=30.
∵ 纸带宽为15,∴ sin∠ABM =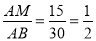 .∴∠AMB=30°.
.∴∠AMB=30°.
【题型】解答题
【结束】
11
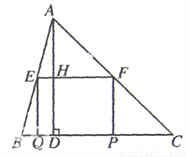
如图,在△ABC中,∠C=45°,BC=10,高AD=8,矩形EFPQ的一边QP在BC边上,E、F两点分别在AB、AC上,AD交EF于点H.
(1)求证: 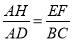 ;
;
(2)设EF=x,当x为何值时,矩形EFPQ的面积最大?并求其最大值;
(3)当矩形EFPQ的面积最大时,该矩形EFPQ以每秒1个单位的速度沿射线QC匀速运动(当点Q与点C重合时停止运动),设运动时间为t秒,矩形EFFQ与△ABC重叠部分的面积为S,求S与t的函数关系式.
查看答案和解析>>
科目:初中数学 来源:黄金30题系列 九年级数学 大题易丢分 题型:解答题
设a是方程x2﹣2006x+1=0的一个根,求代数式a2﹣2007a+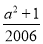 的值.
的值.
查看答案和解析>>
科目:初中数学 来源:黄金30题系列 七年级数学 小题易丢分 题型:填空题
小李用围棋子排成下列一组有规律的图案,其中第1个图案有1枚棋子,第2个图案有3枚棋子,第3个图案有4枚棋子,第4个图案有6枚棋子,…,那么第9个图案的棋子数是___枚.

查看答案和解析>>
科目:初中数学 来源:黄金30题系列 七年级数学 小题易丢分 题型:填空题
已知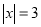 ,
, 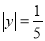 ,且
,且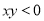 ,则
,则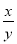 的值等于__________
的值等于__________
查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题八年级人教版数学试卷(A卷) 题型:解答题
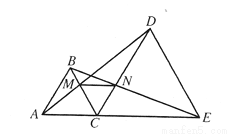
如图,C是线段AE上一点,△ABC、△CDE都是等边三角形,AD与BC交于点M,BE与CD交于点N。
试说明:(1)AD=BE;(2)MN//AE。
查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题八年级北师大版数学试卷(B卷) 题型:单选题
如图, 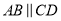 ,
, 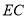 交
交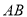 于点
于点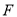 ,
, 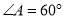 ,
, 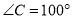 ,则
,则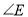 的大小为( ).
的大小为( ).
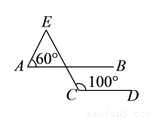
A. 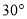 B.
B. 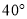 C.
C. 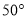 D.
D. 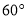
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com