练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    若将三个数－， ， 表示在数轴上，其中能被如图所示的墨迹覆盖的数是（ 　）

    A. － B. C. D. 和

    B 【解析】∵墨迹覆盖的数在1～3， 即～， ∴符合条件的数是． 故选B．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：山东省2017-2018学年七年级上学期期末考试数学试卷 题型：解答题

    学完一元一次方程解法，数学老师出了一道解方程题目：

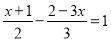    ．李铭同学的解题步骤如下：

    【解析】
    去分母，得3(x＋1)－2(2－3x)＝1；……①

    去括号，得3x＋3－4－6x＝1； ……②

    移项，得3x－6x＝1－3＋4； ……③

    合并同类项，得－3x＝2； ……④

    系数化为1，得x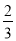＝－． ……⑤

    （1）聪明的你知道李铭的解答过程在第_________(填序号）出现了错误，出现上面错误的原因是违背了____.（填序号）①去括号法则；②等式的性质1；③等式的性质2；④加法交换律．

    （2）请你写出正确的解答过程．

    【解析】 （1）①②，③① ；（2）x＝. 【解析】试题分析：李铭的解法出错在第①、②步，去分母时1没有乘以6，去括号时有一项没变号，方程去分母，去括号，移项合并，把x系数化为1，即可求出解． 试题解析：（1）①②,③① （2）【解析】 去分母，得3(x＋1)－2(2－3x)＝6；……① 去括号，得3x＋3－4+6x＝6； ……② 移项，得3x+6x＝6－3＋4；...

    查看答案和解析>>

    科目：初中数学 来源：北京市丰台区2018届九年级第一学期期末数学试卷 题型：填空题

    如果sinα =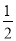，那么锐角α =_____.

    30° 【解析】∵sin30°= ， ∴α=30°， 故答案为：30°.

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年七年级数学下册（人教版）：期中检测题 题型：填空题

    如图，四边形ABCD中，点M，N分别在AB，BC上，将△BMN沿MN翻折，得△FMN，若MF∥AD，FN∥DC，则∠B＝__________．

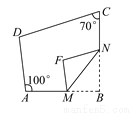
    95°． 【解析】根据平行线性质求出∠BMF和∠BNF，根据翻折得出全等，根据全等三角形性质得出∠BMN=∠FMB=50°，∠BNM =∠FNM=35°，根据三角形内角和定理即可求出答案． 【解析】 ∵MF∥AD,FN∥DC,∠A=100°,∠C=70°， ∴∠FMB=∠A=100°,∠FNB=∠C=70°， ∵△BMN沿MN翻折，得△FMN， ∴△BMN≌△FMN...

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年七年级数学下册（人教版）：期中检测题 题型：单选题

    如图，已知正方形ABCD，定点A（1，3），B（1，1），C（3，1），规定“把正方形ABCD先沿x轴翻折，再向左平移1个单位长度”为一次变换，如此这样，连续经过2 017次变换后，正方形ABCD的对角线交点M的坐标变为（　　）

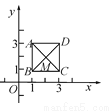
    A. （－2015，2） B. （－2015，－2） C. （－2016，－2） D. （－2016，2）

    B 【解析】由正方形ABCD，顶点A（1，3）、B（1，1）、C（3，1），然后根据题意求得第1次、2次、3次变换后的对角线交点M的对应点的坐标，即可得规律：第n次变换后的点M的对应点的为：当n为奇数时为（2-n，-2），当n为偶数时为（2-n，2），继而求得把正方形ABCD连续经过2017次这样的变换得到正方形ABCD的对角线交点M的坐标． 解答： ∵正方形ABCD,顶点A(1...

    查看答案和解析>>

    科目：初中数学 来源：山东省2018届九年级上学期期末考试数学试卷 题型：解答题

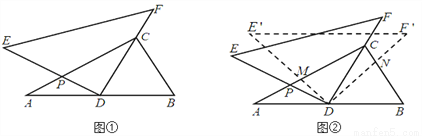
    将一副三角尺（在Rt△ABC中，∠ACB=90°，∠B=60°；在Rt△DEF中，∠EDF=90°，∠E=45°）如图①摆放，点D为AB的中点，DE交AC于点P，DF经过点C.

    （1）求∠ADE的度数；

    （2）如图②，将△DEF绕点D顺时针方向旋转角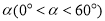，此时等腰直角三角尺记为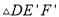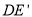， 交AC于点M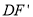， 交BC于点N，试判断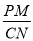的值是否随着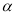的变化而变化？如果不变，请求出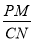的值；反之，请说明理由.

    （1）∠ADE=30°；（2）不变化，理由见解析. 【解析】将一副三角尺（在Rt△ABC中，∠ACB=90°，∠B=60°；在Rt△DEF中，∠EDF=90°，∠E=45°）如图①摆放，点D为AB的中点，DE交AC于点P，DF经过点C. （1）求∠ADE的度数； （2）如图②，将△DEF绕点D顺时针方向旋转角（0°＜＜60°），此时等腰直角三角尺记为， 交AC于点M， 交BC于点...

    查看答案和解析>>

    科目：初中数学 来源：山东省2018届九年级上学期期末考试数学试卷 题型：填空题

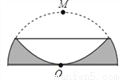
    如图，半径为2的半圆形纸片，按如图方式折叠，使对折后半圆弧的中点M与圆心O重合，则图中阴影部分的面积是___________.

    【解析】试题解析：如图，连接OM交AB于点C，连接OA、OB， 由题意知，OM⊥AB，且OC=MC=1， 在RT△AOC中，∵OA=2，OC=1， ∴cos∠AOC=，AC= ∴∠AOC=60°，AB=2AC=2， ∴∠AOB=2∠AOC=120°， 则S弓形ABM=S扇形OAB-S△AOB = =， S阴影=S半圆-2S弓形ABM =π...

    查看答案和解析>>

    科目：初中数学 来源：山东省2018届九年级上学期期末考试数学试卷 题型：单选题

    计算： 的值为（ ）

    A. B. C. D.

    C 【解析】试题解析： = = =1. 故选C.

    查看答案和解析>>

    科目：初中数学 来源：四川省自贡市2017－2018学年上学期七年级期末统一考试数学试卷 题型：填空题

    要在A、B两个村庄之间建一个车站，则当车站建在A、B村庄之间的线段上时，它到两个村庄的路程和最短，理由是________________.

    两点之间，线段最短 【解析】将A，B两个村庄看作平面内的两个点，并设代表车站的点为点C，则根据两点之间距离的定义，车站C到两个村庄的路程分别为线段CA与线段CB的长度. 车站到两个村庄的路程和可以表示为CA+CB. 根据“两点之间，线段最短”，在点A与点B的所有连线中，线段AB是最短的. 因此，要使CA+CB最小，则CA+CB=AB. 要使CA+CB=AB，则车站只能建在村庄A与村庄B...

    查看答案和解析>>

    同步练习册答案