
按下列程序进行计算,经过三次输入,最后输出的数是10,则最初输入的数是

A. 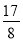 B.
B. 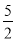 C. 4 D.
C. 4 D. 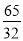
 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:初中数学 来源:江苏省扬州市宝应县2018届九年级上学期12月月考数学试卷 题型:解答题
如图,梯形ABCD中,AD∥BC,对角线AC、BD交于点O,BE∥CD交CA延长线于E 求证:
(1)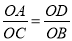 ;(2)
;(2)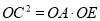
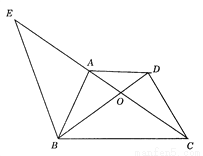
查看答案和解析>>
科目:初中数学 来源:江苏省泰州市2017年中考数学二模试卷(解析版) 题型:单选题
如图,在平面直角坐标系xOy中,△A′B′C′由△ABC绕点P旋转得到,则点P的坐标为( )
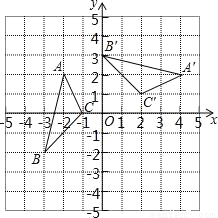
A.(0,1) B.(1,-1) C.(0,-1) D.(1,0)
B. 【解析】 试题解析:由图形可知,对应点的连线CC′、AA′的垂直平分线的交点是点(1,-1),根据旋转变换的性质,点(1,-1)即为旋转中心. 故旋转中心坐标是P(1,-1). 故选B.查看答案和解析>>
科目:初中数学 来源:2017年河南省中考数学三模试卷 题型:单选题
(3分)在学校开展的“争做最优秀中学生”的一次演讲比赛中,编号1,2,3,4,5的五位同学最后成绩如表所示:那么这五位同学演讲成绩的众数与中位数依次是( )
参赛者编号 | 1 | 2 | 3 | 4 | 5 |
成绩/分 | 96 | 88 | 86 | 93 | 86 |
A. 96,88 B. 86,88 C. 88,86 D. 86,86
B 【解析】【解析】 ∵这组数据中86出现的次数最多,是2次, ∴这五位同学演讲成绩的众数是86; 这五位同学演讲成绩的中位数是88, ∴这五位同学演讲成绩的众数与中位数依次是86,88. 故选:B.查看答案和解析>>
科目:初中数学 来源:湖北省黄冈市2017-2018学年七年级上学期第三次学力检测数学试卷 题型:单选题
下列算式中,结果是正数的是( )
A. -[-(-3)] B. -|-(-3)|3
C. -(-3)2 D. -32×(-2)3
D 【解析】A选项:-[-(-3)]=-[+3]=-3,故A错误; B选项:-|-(-3)|3=-27,故B错误; C选项:-(-3)2=-9,故C错误; D选项:-32×(-2)3=-9×(-8)=72,故D正确; 故选D.查看答案和解析>>
科目:初中数学 来源:浙江杭州西湖区保俶塔实验学校2018届九年级上学期期中考试数学试卷(含解析) 题型:解答题
甲、乙、丙三人之间相互传球,球从一个人手中随机传到另一个人手中,
( )若开始时球在甲手中,求经过三次传球后,球传回到甲手中的概率是多少?(用列表法或树状图法说明)
)若开始时球在甲手中,求经过三次传球后,球传回到甲手中的概率是多少?(用列表法或树状图法说明)
( )若乙想使球经过三次传递后,球落在自己手中的概率最大,乙会让球开始时在谁手中?
)若乙想使球经过三次传递后,球落在自己手中的概率最大,乙会让球开始时在谁手中?
查看答案和解析>>
科目:初中数学 来源:浙江杭州西湖区保俶塔实验学校2018届九年级上学期期中考试数学试卷(含解析) 题型:单选题
将抛物线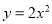 先向左平移一个单位,再向上平移一个单位,两次平移后得到的抛物线解析式为( ).
先向左平移一个单位,再向上平移一个单位,两次平移后得到的抛物线解析式为( ).
A. 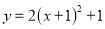 B.
B. 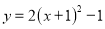 C.
C. 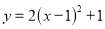 D.
D. 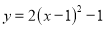
查看答案和解析>>
科目:初中数学 来源:浙江省宁波市2017-2018学年八年级上册期末模拟数学试卷 题型:单选题
下列三角形不一定全等的是( )
A. 面积相等的两个三角形
B. 周长相等的两个等边三角形
C. 斜边和一条直角边分别对应相等的两个直角三角形
D. 有一个角是100°,腰长相等的两个等腰三角形
A 【解析】A、如果△ABC和△DEF中,BC=1,BC上的高AD=2,△DEF的边EF=2,EF上的高是1,两三角形的面积相等,但△ABC和△DEF不一定全等,故本选项正确; B、△ABC和△DEF,AB=BC=AC,DE=EF=DF,根据周长相等,则AB=BC=AC=DE=DF=EF,根据SSS即可推出两三角形全等,故本选项错误; C、根据直角三角形全等的判定定理HL,推出两...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com