
计算:
(1)(-12)-5+(-14)-(-39)
(2)-32÷(-3)2+3×(-2)+|-4|.
(1)8(2)-3 【解析】(1)首先对式子进行化简,然后正负数分别相加,最后把所得的结果相加即可; (2)原式先计算乘方运算,再计算乘除运算,最后算加减运算即可得到结果 【解析】 (1)原式=-12-5-14+39=-31+39=8. (2)原式=-9÷9-6+4=-1-6+4=-3.科目:初中数学 来源:上海浦东新区2017-2018学年九年级上学期期末数学试卷(初三一模) 题型:解答题
将抛物线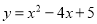 向左平移4个单位,求平移后抛物线的表达式、顶点坐标
向左平移4个单位,求平移后抛物线的表达式、顶点坐标
和对称轴.
,顶点坐标是(-2,1);对称轴是直线. 【解析】试题分析:平移抛物线的依据是,当二次函数的二次项系数a的值相同时,二次函数图像的形状完全相同,即开口方向和开口大小完全相同,仅仅位置不同,所以他们之间可以进行平移. 试题解析:∵=, ∴平移后的函数解析式是. 顶点坐标是(-2,1). 对称轴是直线.查看答案和解析>>
科目:初中数学 来源:2017-2018学年度第一学期海南省海口市九年级数学科期末检测题 题型:解答题
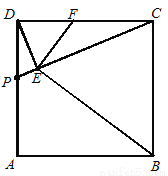
如图,正方形ABCD中,点P是AD上的一动点(与点D、点A不重合),DE⊥CP,垂足为E,EF⊥BE与DC交于点F.
(1)求证:△DEF∽△CEB;
(2)当点P运动到DA的中点时,求证:点F为DC的中点.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年度第一学期海南省海口市九年级数学科期末检测题 题型:单选题
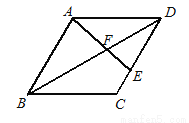
如图,□ABCD中,点E在CD上,AE交BD于点F,若DE =2CE,则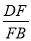 等于( )
等于( )
A. 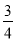 B.
B. 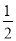 C.
C. 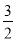 D.
D. 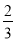
查看答案和解析>>
科目:初中数学 来源:安徽省2017-2018学年度七年级第一学期人教版数学期末自测试卷(二) 题型:解答题
如图1,长方形OABC的边OA在数轴上,O为原点,长方形OABC的面积为12,OC边长为3.

(1)数轴上点A表示的数为________.
(2)将长方形OABC沿数轴水平移动,移动后的长方形记为O′A′B′C′,移动后的长方形O′A′B′C′与原长方形OABC重叠部分(如图2中阴影部分)的面积记为S.
①当S恰好等于原长方形OABC面积的一半时,数轴上点A′表示的数是多少?
②设点A的移动距离AA′=x.
(ⅰ)当S=4时,求x的值;
(ⅱ)D为线段AA′的中点,点E在线段OO′上,且OE=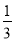 OO′,当点D,E所表示的数互为相反数时,求x的值.
OO′,当点D,E所表示的数互为相反数时,求x的值.
查看答案和解析>>
科目:初中数学 来源:安徽省2017-2018学年度七年级第一学期人教版数学期末自测试卷(二) 题型:填空题
若5xm+1y5与3x2y2n+1是同类项,则m=________,n=________.
1 2 【解析】根据同类项的定义,得出关于m,n的方程,求出m,n的值. 【解析】 ∵单项式5xm+1y5与3x2y2n+1是同类项, ∴m+1=2,m=1,2n+1=5, n=2, 故答案为:1,2. “点睛”本题考查了同类项的知识,解答本题的关键是掌握同类项定义中的两个“相同”:相同字母的指数相同.查看答案和解析>>
科目:初中数学 来源:安徽省2017-2018学年度七年级第一学期人教版数学期末自测试卷(二) 题型:单选题
如果以x=-5为方程的解构造一个一元一次方程,那么下列方程中不满足要求的是( )
A. x+5=0 B. x-7=-12
C. 2x+5=-5 D. 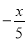 =-1
=-1
查看答案和解析>>
科目:初中数学 来源:内蒙古赤峰市宁城县2017-2018学年八年级上学期期末考试数学试卷 题型:填空题
已知m2-2m-1=0,则代数式2m2-4m+2017的值为_______________.
2019 【解析】因为m2-2m-1=0,所以m2-2m=1,所以2m2-4m=2(m2-2m)=2,所以2m2-4m+2017=2+2017=2019,故答案为:2019.查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期初三数学期末试卷 题型:解答题
在等腰△ABC中,AB=AC,将线段BA绕点B顺时针旋转到BD,使BD⊥AC于H,连结AD并延长交BC的延长线于点P.
(1)依题意补全图形;
(2)若∠BAC=2α,求∠BDA的大小(用含α的式子表示);
(3)小明作了点D关于直线BC的对称点点E,从而用等式表示线段DP与BC之间的数量关系.请你用小明的思路补全图形并证明线段DP与BC之间的数量关系.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com