
某一公路的道路维修工程,准备从甲、乙两个工程队选一个队单独完成.根据两队每天的工程费用和每天完成的工程量可知,若由两队合做此项维修工程,6天可以完成,共需工程费用385200元,若单独完成此项维修工程,甲队比乙队少用5天,每天的工程费用甲队比乙队多4000元,(1)若甲单独完成需要多少天?(2)从节省资金的角度考虑,应该选择哪个工程队?
(1)甲队单独完成此项工程需要10天;(2)从节省资金的角度考虑,应该选择甲工程队. 【解析】试题分析:设甲队单独完成此项工程需要x天,乙队单独完成需要(x+5)天,然后依据6天可以完成,列出关于x的方程,从而可求得甲、乙两队单独完成需要的天数,然后设甲队每天的工程费为y元,则可表示出乙队每天的工程费,接下来,根据两队合作6天的工程费用为385200元列方程求解,于是可得到两队独做一天各自的... 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源:山东省2017-2018学年七年级上期末复习检测数学试卷 题型:填空题
比较大小:﹣π________﹣3.14; 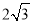 ________
________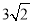 .
.
查看答案和解析>>
科目:初中数学 来源:重庆市江北区2018届九年级上期末模拟数学试卷 题型:单选题
下列图形中,既是轴对称图形又是中心对称图形的是( )
A.  B.
B. 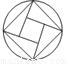 C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源:2017年辽宁省营口市大石桥市水源镇中考数学模拟试卷(三) 题型:单选题
如图,抛物线y1=a(x+2)2﹣3与y2=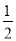 (x﹣3)2+1交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于点B,C.则以下结论:
(x﹣3)2+1交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于点B,C.则以下结论:
①无论x取何值,y2的值总是正数;
②a=1;
③当x=0时,y2﹣y1=4;
④2AB=3AC;
其中正确结论是( )
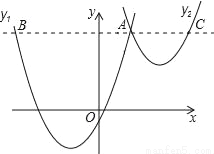
A. ①② B. ②③ C. ③④ D. ①④
D 【解析】试题解析::①∵抛物线y2=(x-3)2+1开口向上,顶点坐标在x轴的上方,∴无论x取何值,y2的值总是正数,故本结论正确; ②把A(1,3)代入,抛物线y1=a(x+2)2-3得,3=a(1+2)2-3,解得a=,故本结论错误; ③由两函数图象可知,抛物线y1=a(x+2)2-3解析式为y1=(x+2)2-3,当x=0时,y1=(0+2)2-3=-,y2=(0-3)...查看答案和解析>>
科目:初中数学 来源:2017年辽宁省营口市大石桥市水源镇中考数学模拟试卷(三) 题型:单选题
下列式子中正确的是( )
A. (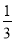 )﹣2=﹣9 B. (﹣2)3=﹣6 C.
)﹣2=﹣9 B. (﹣2)3=﹣6 C. 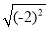 =﹣2 D. (﹣3)0=1
=﹣2 D. (﹣3)0=1
查看答案和解析>>
科目:初中数学 来源:2017年湖南省郴州市资兴市兴华实验学校中考数学模拟试卷 题型:解答题
已知:y=y1+y2,y1与x2成正比例,y2与x成反比例,且x=1时,y=3;x=﹣1时,y=1.求x=﹣ 时,y的值.
时,y的值.
查看答案和解析>>
科目:初中数学 来源:2017年湖南省郴州市资兴市兴华实验学校中考数学模拟试卷 题型:填空题
如图,AB∥CD,直线EF分别交AB、CD于M,N两点,将一个含有45°角的直角三角尺按如图所示的方式摆放,若∠EMB=75°,则∠PNM等于_____度.
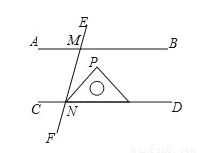
查看答案和解析>>
科目:初中数学 来源:辽宁省抚顺县2017-2018学年八年级上学期期末教学质量检测数学试卷 题型:解答题
先化简,再求值: 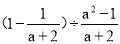 ,其中a=3.
,其中a=3.
查看答案和解析>>
科目:初中数学 来源:江苏省扬州市邗江区2018届九年级(上)期中数学试卷 题型:单选题
对于一元二次方程ax2+bx+c=0 (a≠0),下列说法中错误的是( )
A. 当a>0,c<0时,方程一定有实数根
B. 当c=0时,方程至少有一个根为0
C. 当a>0,b=0,c<0时,方程的两根一定互为相反数
D. 当abc<0时,方程的两个根同号,当abc>0时,方程的两个根异号
D 【解析】解:A.正确.当a>0,c<0时,△=b2﹣4ac>0,则方程一定有实数根; B.正确.当c=0时,则ax2+bx=0,则方程至少有一个根为0; C.正确.当a>0,b=0,c<0时,方程两根为x1,x2,x1+x2==0,则方程的两根一定互为相反数; D.错误.当ac<0时,方程的两个根异号,当ac>0时,方程的两个根同号. 故选D.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com