练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

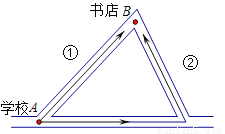
    如图，从学校A到书店B最近的路线是①号路线，得出这个结论的根据是：__________________

    两点之间，线段最短 【解析】从学校A到书店B最近的路线是①号路线，得到这个结论的根据是两点之间，线段最短， 故答案为：两点之间，线段最短．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：内蒙古赤峰市宁城县2018届九年级上学期期末数学试卷 题型：单选题

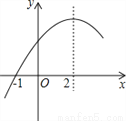
    二次函数y=ax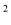+bx+c（a≠0）的部分图象如图，图象过点（-1，0），对称轴为直线x=2，下列结论：①抛物线与x轴的另一个交点是（5，0）；②4a+c＞2b；③4a+b=0；④当x＞-1时，y的值随x值的增大而增大．其中正确的结论有（　　）

    A. 1个 B. 2个 C. 3个 D. 4个

    B 【解析】试题解析：①∵二次函数y=ax2+bx+c（a≠0）与x轴的一个交点为（-1，0）且对称轴为直线x=2， ∴另一个交点坐标为（5，0），故①正确； ②∵二次函数y=ax2+bx+c（a≠0）的部分图象如图所示，图象过点（-1，0），对称轴为直线x=2， ∴当x=-2时，y=4a-2b+c＜0， ∴4a+c＜2b，故②错误； ③∵对称轴为=-， ∴?=2， ...

    查看答案和解析>>

    科目：初中数学 来源：贵州省贵阳市2017-2018学年七年级（上）期末模拟数学试卷 题型：解答题

    把下面的直线补充成一条数轴，并把下列各数在数轴上表示出来，再按从小到大的顺序用“＜”连接起来：﹣3，0，+3.5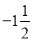， ，0.5．

    答案见解析． 【解析】试题分析：根据数轴是表示数的一条直线，可把数在数轴上表示出来，根据数轴上的点表示的数右边的总比左边的大，可得答案． 试题解析：如图： ； 数轴上的点表示的数右边的总比左边的大，得 ﹣3＜﹣1＜0＜0.5＜+3.5．

    查看答案和解析>>

    科目：初中数学 来源：贵州省贵阳市2017-2018学年七年级（上）期末模拟数学试卷 题型：单选题

    下列小数可用科学记数法表示为8.02×10﹣5的是（　　）

    A. 0.00000802 B. 0.0000802 C. 0.00802 D. 802000

    B 【解析】科学记数法的表示形式为a×10n的形式，其中1≤|a|<10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值>1时，n是正数；当原数的绝对值<1时，n是负数， 8.02×10﹣5=0.0000802， 故选B．

    查看答案和解析>>

    科目：初中数学 来源：云南省2016-2017学年七年级上学期期末考试数学试卷 题型：解答题

    先化简,再求值: 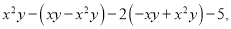其中.

    xy-5 -7 【解析】试题分析：本题要先去括号再合并同类项，对原代数式进行化简，然后把x，y的值代入计算即可． 试题解析：原式= = 当，y=2时 ，原式=-1×2-5=-7.

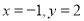    查看答案和解析>>

    科目：初中数学 来源：云南省2016-2017学年七年级上学期期末考试数学试卷 题型：单选题

    有理数a，b在数轴上对应点的位置如图所示，下列各式正确的是（　　）

    A. a+b＜0 B. a﹣b＜0 C. a•b＞0 D. 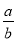＞0

    B 【解析】：由a，b在数轴上对应点的位置如图所示，得a＜0＜b，|a|＜|b|， A、a+b＜0，故A不符合题意；由a，b在数轴上对应B、a﹣b＜0，故B符合题意；C、a•b＞0，故C不符合题意；D、＜0，故D不符合题意； 故选：B．

    查看答案和解析>>

    科目：初中数学 来源：云南省2016-2017学年七年级上学期期末考试数学试卷 题型：单选题

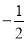    的相反数是（ ）

    A. 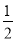B. 2 C. -2 D. －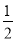

    A 【解析】只有符号不同的两个数叫做互为相反数， 所以的相反数是， 故选A.

    查看答案和解析>>

    科目：初中数学 来源：江苏省扬州市2016-2017学年七年级上学期期末考试数学试卷 题型：填空题

    已知∠A=35°10′48″，则∠A的余角是__________．

    54°49′12″ 【解析】如果两个角的和为90°，那么这两个角互余，由此可得∠A的余角为：90°-35°10′48″=54°49′12″.

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年七年级数学下册（遵义）：期中检测题 题型：解答题

    如图，已知∠ABC＝∠ADC，BF，DE分别平分∠ABC与∠ADC，∠1＝∠3，试说明：AB∥DC.

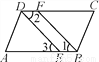
    证明见解析 【解析】试题分析：先根据角平分线定义可证明∠1=∠2，进而利用平行线的判定方法得出答案． 试题解析：证明：∵BF平分∠ABC，∴∠1＝∠FBC. ∵DE平分∠ADC，∴∠2＝∠ADE. ∵∠ABC＝∠ADC，∴∠1＋∠FBC＝∠2＋∠ADE， ∴2∠1＝2∠2，即∠1＝∠2. 又∵∠1＝∠3，∴∠2＝∠3， ∴AB∥DC.

    查看答案和解析>>

    同步练习册答案