
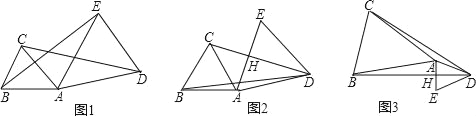
已知△ABC中,AB=AC.
(1)如图1,在△ADE中,若AD=AE,且∠DAE=∠BAC,求证:CD=BE;
(2)如图2,在△ADE中,若∠DAE=∠BAC=60°,且CD垂直平分AE,AD=3,CD=4,求BD的长;
(3)如图3,在△ADE中,当BD垂直平分AE于H,且∠BAC=2∠ADB时,试探究CD2,BD2,AH2之间的数量关系,并证明.
科目:初中数学 来源:四川省资阳市安岳县2018届中考数学二模试卷 题型:填空题
如图,在正方形ABCD中,点E,N,P,G分别在边AB,BC,CD,DA上,点M,F,Q都在对角线BD上,且四边形MNPQ和AEFG均为正方形,则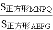 的值等于_____.
的值等于_____.
查看答案和解析>>
科目:初中数学 来源:山东省日照市2018届九年级上期10月月考数学试卷 题型:解答题
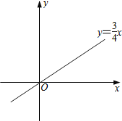
一次函数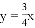 的图象如图所示,它与二次函数
的图象如图所示,它与二次函数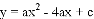 的图象交于
的图象交于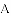
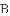
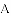
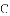
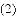
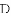
①若点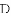
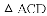
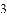
②若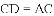
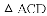
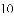
查看答案和解析>>
科目:初中数学 来源:山东省日照市2018届九年级上期10月月考数学试卷 题型:单选题
已知正方形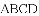
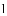
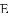
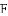
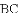
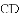
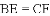
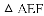
A. 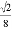 B.
B. 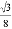 C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源:山东省日照市2018届九年级上期10月月考数学试卷 题型:单选题
对于抛物线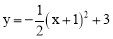 ,下列结论:①抛物线的开口向下;②对称轴为直线x=1;③顶点坐标为(-1,3);④x>1时,y随x的增大而减小,其中正确结论的个数为
,下列结论:①抛物线的开口向下;②对称轴为直线x=1;③顶点坐标为(-1,3);④x>1时,y随x的增大而减小,其中正确结论的个数为
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:初中数学 来源:北师大版八年级上册 第1章《勾股定理》单元检测C卷 题型:解答题
如图,在4×4正方形网格中,每个小正方形的边长都为1.
(1)求△ABC的周长;
(2)求证:∠ABC=90°.

查看答案和解析>>
科目:初中数学 来源:北师大版八年级上册 第1章《勾股定理》单元检测C卷 题型:单选题
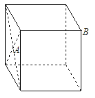
如图,点A的正方体左侧面的中心,点B是正方体的一个顶点,正方体的棱长为2,一蚂蚁从点A沿其表面爬到点B的最短路程是( )
A. 3 B. 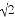 +2 C.
+2 C. 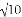 D. 4
D. 4
查看答案和解析>>
科目:初中数学 来源:内蒙古赤峰市联盟校会2018届九年级中考一模数学试卷 题型:解答题
已知抛物线与x轴的交点坐标分别为A(1,0),B(x2,0)(点B在点A的右侧),其对称轴是x=3,该函数有最小值是﹣2.
(1)求二次函数解析式;
(2)在图1上作平行于x轴的直线,交抛物线于C(x3,y3),D(x4,y4),求x3+x4的值;
(3)将(1)中函数的部分图象(x>x2)向下翻折与原图象未翻折的部分组成图象“G”,如图2,在(2)中平行于x轴的直线取点E(x5,y5)、(x4<x5),结合函数图象求x3+x4+x5的取值范围.
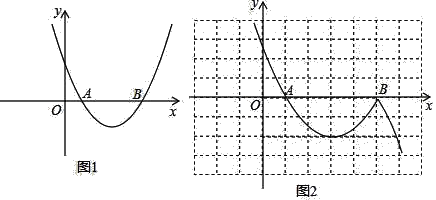
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com