
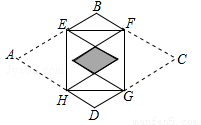
如图,矩形EFGH的四个顶点分别在菱形ABCD的四条边上,BE=BF,将△AEH,△CFG分别沿边EH,FG折叠,当重叠部分为菱形且面积是菱形ABCD面积的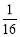 时,则
时,则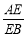 为( )
为( )
A. 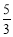 B.2 C.
B.2 C. 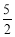 D.4
D.4
科目:初中数学 来源:2017年初中毕业升学考试(重庆A卷)数学(解析版) 题型:选择题
下列图形都是由同样大小的菱形按照一定规律所组成的,其中第①个图形中一共有3个菱形,第②个图形中一共有7个菱形,第③个图形中一共有13个菱形,…,按此规律排列下去,第⑨个图形中菱形的个数为( )
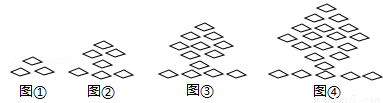
A.73 B.81 C.91 D.109
查看答案和解析>>
科目:初中数学 来源:2017年初中毕业升学考试(浙江温州卷)数学(解析版) 题型:填空题
小明家的洗手盆上装有一种抬启式水龙头(如图1),完全开启后,水流路线呈抛物线,把手端点A,出水口B和落水点C恰好在同一直线上,点A至出水管BD的距离为12cm,洗手盆及水龙头的相关数据如图2所示,现用高10.2cm的圆柱型水杯去接水,若水流所在抛物线经过点D和杯子上底面中心E,则点E到洗手盆内侧的距离EH为_________cm.
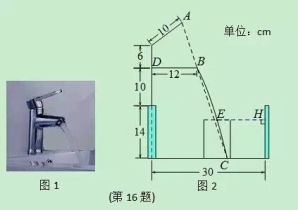
(第16题图)
查看答案和解析>>
科目:初中数学 来源:2017年初中毕业升学考试(浙江台州卷)数学(解析版) 题型:解答题
交通工程学理论把在单向道路上行驶的汽车看成连续的流体,并用流量、速度、密度三个概念描述车流的基本特征,其中流量q(辆/小时)指单位时间内通过道路指定断面的车辆数;速度v(千米/小时)指通过道路指定断面的车辆速度,密度k(辆/千米)指通过道路指定断面单位长度内的车辆数.
为配合大数据治堵行动,测得某路段流量q与速度v之间关系的部分数据如下表:

(1)根据上表信息,下列三个函数关系式中,刻画q,v关系最准确的是 (只填上正确答案的序号)
①q=90v+100;②q=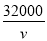 ;③
;③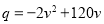 .
.
(2)请利用(1)中选取的函数关系式分析,当该路段的车流速度为多少时,流量达到最大?最大流量是多少?
(3)已知q,v,k满足q=vk,请结合(1)中选取的函数关系式继续解决下列问题.
①市交通运行监控平台显示,当12≤v<18时道路出现轻度拥堵.试分析当车流密度k在什么范围时,该路段将出现轻度拥堵;
②在理想状态下,假设前后两车车头之间的距离d(米)均相等,求流量q最大时d的值.
查看答案和解析>>
科目:初中数学 来源:2017年初中毕业升学考试(浙江台州卷)数学(解析版) 题型:填空题
三名运动员参加定点投篮比赛,原定出场顺序是:甲第一个出场,乙第二个出场,丙第三个出场,由于某种原因,要求这三名运动员用抽签方式重新确定出场顺序,则抽签后每个运动员的出场顺序都发生变化的概率为 .
查看答案和解析>>
科目:初中数学 来源:2017年初中毕业升学考试(浙江台州卷)数学(解析版) 题型:选择题
如图,点P是∠AOB平分线OC上一点,PD⊥OB,垂足为D,若PD=2,则点P到边OA的距离是( )
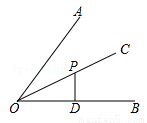
A.2 B.3 C.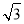 D.4
D.4
查看答案和解析>>
科目:初中数学 来源:2017年初中毕业升学考试(浙江绍兴卷)数学(解析版) 题型:解答题
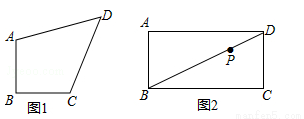
定义:有一组邻边相等,并且它们的夹角是直角的凸四边形叫做等腰直角四边形.
(1)如图1,等腰直角四边形ABCD,AB=BC,∠ABC=90°.
①若AB=CD=1,AB∥CD,求对角线BD的长.
②若AC⊥BD,求证:AD=CD;
(2)如图2,在矩形ABCD中,AB=5,BC=9,点P是对角线BD上一点,且BP=2PD,过点P作直线分别交边AD,BC于点E,F,使四边形ABFE是等腰直角四边形,求AE的长.
查看答案和解析>>
科目:初中数学 来源:2017年初中毕业升学考试(浙江绍兴卷)数学(解析版) 题型:选择题
下表记录了甲、乙、丙、丁四名射击运动员最近几次选拔赛成绩的平均数和方差:
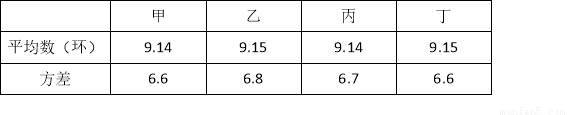
根据表中数据,要从中选择一名成绩好且发挥稳定的运动员参加比赛,应选择( )
A.甲 B.乙 C.丙 D.丁
查看答案和解析>>
科目:初中数学 来源:九年级数学(浙教版)上册同步练习:2.1 事件的可能性(二) 题型:单选题
掷一枚质地均匀的硬币10次,下列说法中,正确的是( )
A. 有5次正面朝上
B. 不可能10次正面朝上
C. 不可能10次正面朝下
D. 可能有5次正面朝上
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com