
��ͼ���ڡ�ABC�͡�DEC�У���ABC=��DEC=90�㣬����AD������EB��F��AC��DE���ӳ�CA������EB�ڵ�G����Fǡ����AD�е㡣
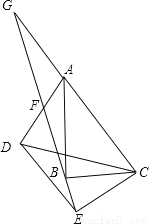
��1����֤����AFG�ա�DFE��
��2����BC=CE��
����֤����ABF=��DEF��
������BAC=30�㣬�����AFG�Ķ�����
 ��1��֤����������2����֤���������ڡ�AFG=60�㡣
�����������������
��1����AG��DE�ã���G=��DEF����F��AD���е���AF=DF����ϡ�AFG=��DFE������֤�ã���AGF�ա�DEF��
��2������BC=CE�ɵá�CBE=��CEB����ϡ�ABC=DEC=90�㣬�á�ABF+��CBE=90�㣬��CEB+��DEF=90�㣬�Ӷ��ɵá�ABF=��DEF��
���ɡ�A...
��1��֤����������2����֤���������ڡ�AFG=60�㡣
�����������������
��1����AG��DE�ã���G=��DEF����F��AD���е���AF=DF����ϡ�AFG=��DFE������֤�ã���AGF�ա�DEF��
��2������BC=CE�ɵá�CBE=��CEB����ϡ�ABC=DEC=90�㣬�á�ABF+��CBE=90�㣬��CEB+��DEF=90�㣬�Ӷ��ɵá�ABF=��DEF��
���ɡ�A...  �������Ӧ���⼯ѵϵ�д�
�������Ӧ���⼯ѵϵ�д� �ۺ��Բ�ϵ�д�
�ۺ��Բ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ����ʦ�����꼶�²� �ڶ��¡�һԪһ�β���ʽ�� һԪһ�β���ʽ�� 2.4��һԪһ�β���ʽ ͬ����ϰ�� ���� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ����ʦ�����꼶�²� �ڶ��¡�һԪһ�β���ʽ�� һԪһ�β���ʽ�� 2.4��һԪһ�β���ʽ ͬ����ϰ�� ���� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ����ʦ������꼶��ѧ�²�4.3.3̽��������ȫ�ȵ�������ϰ ���ͣ������
��ͼ����ABC�͡�AED�У���BAC=��DAE��AB=AE��AC=AD������BD��CE����֤��BD=EC��
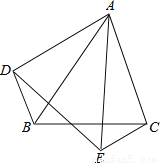
 ֤��������
�����������������
�ɡ�BAC=��DAE�á�BAD=��EAC�����AB=AE��AC=AD�������ɡ�SAS��֤�ã���BAD�ա�EAC���Ӷ��ɵã�BD=EC.
���������
�ߡ�DAE=��BAC��
���DAE-��BAE=��EAC-��BAE��
���BAD=��EAC��
�ڡ�BAD�͡�EAC�У�
���BAD�ա�EAC��SAS����
��BD=EC...
֤��������
�����������������
�ɡ�BAC=��DAE�á�BAD=��EAC�����AB=AE��AC=AD�������ɡ�SAS��֤�ã���BAD�ա�EAC���Ӷ��ɵã�BD=EC.
���������
�ߡ�DAE=��BAC��
���DAE-��BAE=��EAC-��BAE��
���BAD=��EAC��
�ڡ�BAD�͡�EAC�У�
���BAD�ա�EAC��SAS����
��BD=EC...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ����ʦ�����꼶��ѧ�²ᵥԪ���ԡ���2�� һԪһ�β���ʽ��һԪһ�β���ʽ�顷 ���ͣ������
С�ܵ�ѧУʳ��������A��B������ǰ���Ŷӵ���һ����(��Ϊa�ˣ�a��8������վ��A���ڶ���ĺ��棬����2���ӣ�������A����ÿ������4�����˷��뿪���飬B����ÿ������6�����˷��뿪���飬��B���ڶ������ÿ��������5�ˣ�
��1����ʱ����С�ܼ�����A�����Ŷӣ��������ﴰ��������ʱ���Ƕ��٣����ú�a�Ĵ���ʽ��ʾ��
��2����ʱ����С��Ѹ�ٴ�A���ڶ���ת�Ƶ�B���ں��������Ŷӣ��ҵ���B����������ʱ��ȼ�����A�����Ŷӵ���A����������ʱ���٣���a��ȡֵ��Χ�����������������أ�
 ��1���֣���2��a��20
��������
�����������1�����ݡ�����2���ӣ�������A����ÿ������4�����˷��뿪���顱�����г�����ʽ��
��2�����ݡ�����B����������ʱ��ȼ�����A�����Ŷӵ���A����������ʱ���١������в���ʽ���.
��1�����������������A�����Ŷӵ��ﴰ��������ʱ��Ϊ�֣�
��2�����������a��20.
��1���֣���2��a��20
��������
�����������1�����ݡ�����2���ӣ�������A����ÿ������4�����˷��뿪���顱�����г�����ʽ��
��2�����ݡ�����B����������ʱ��ȼ�����A�����Ŷӵ���A����������ʱ���١������в���ʽ���.
��1�����������������A�����Ŷӵ��ﴰ��������ʱ��Ϊ�֣�
��2��������ã����a��20.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ����ʦ���°���꼶��ѧ�²ᡶ��2�� һԪһ�β���ʽ���飩��2016�굥Ԫ���Ծ���ɽ��ʡ���������棩 ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com