
解方程:
(1)3x+2=7-2x;
(2)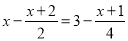 .
.
科目:初中数学 来源:新疆乌鲁木齐市2017-2018学年七年级上学期期末考试数学试卷 题型:填空题
已知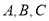 是数轴上的三个点,且
是数轴上的三个点,且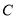 在
在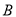 的右侧.点
的右侧.点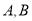 表示的数分别是
表示的数分别是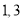 ,若
,若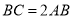 ,则点
,则点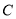 表示的数是__.
表示的数是__.
查看答案和解析>>
科目:初中数学 来源:上海市金山区2018届九年级上学期期末质量检测数学试卷 题型:解答题
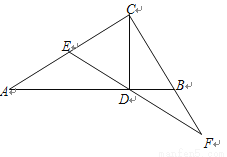
如图,已知在Rt△ABC中,∠ACB=90°,AC > BC,CD是Rt△ABC的高,E是AC的中点,ED的延长线与CB的延长线相交于点F.
(1)求证:DF是BF和CF的比例中项;
(2)在AB上取一点G,如果AE·AC=AG·AD,求证:EG·CF=ED·DF.
查看答案和解析>>
科目:初中数学 来源:上海市金山区2018届九年级上学期期末质量检测数学试卷 题型:单选题
在Rt△ABC中,∠ACB=90°,AC=12,BC=9,D是AB的中点,G是△ABC的重心,如果以点D为圆心DG为半径的圆和以点C为圆心半径为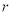 的圆相交,那么
的圆相交,那么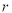 的取值范围是( )
的取值范围是( )
A. 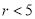 ; B.
; B. 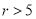 ; C.
; C. 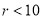 ; D.
; D. 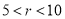 .
.
查看答案和解析>>
科目:初中数学 来源:湖北省武汉市武昌区2017-2018学年七年级上学期期末考试数学试卷 题型:解答题
如图,点B、C在线段AD上,CD=2AB+3.
(1)若点C是线段AD的中点,求BC-AB的值;
(2)若BC=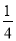 AD,求BC-AB的值;
AD,求BC-AB的值;
(3)若线段AC上有一点P(不与点B重合),AP+AC=DP,求BP的长.
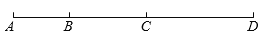
查看答案和解析>>
科目:初中数学 来源:湖北省武汉市武昌区2017-2018学年七年级上学期期末考试数学试卷 题型:填空题
单项式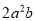 的次数是_________.
的次数是_________.
查看答案和解析>>
科目:初中数学 来源:湖北省武汉市武昌区2017-2018学年七年级上学期期末考试数学试卷 题型:单选题
若x=﹣1是关于x的方程2x+5a=3的解,则a的值为( )
A. 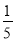 B. 4 C. 1 D. ﹣1
B. 4 C. 1 D. ﹣1
查看答案和解析>>
科目:初中数学 来源:安徽省芜湖市2017-2018学年度第一学期期末考试八年级数学试卷 题型:单选题
下列图形都是按照一定规律组成,第一图形中共有2个三角形,第二图形中共有8个三角形,第三个图形中共有14个三角形,……,依此规律,第六个图形中三角形的个数是( )

A. 32 B. 34 C. 36 D. 40
A 【解析】∵第一图形中共有2个三角形;2=2+6×0; 第二图形中共有8个三角形,8=2+6×1; 第三个图形中共有14个三角形,14=2+6×2; ……, ∴第六个图形中三角形的个数是:2+6×5=32(个).查看答案和解析>>
科目:初中数学 来源:安徽省豪州市心校2017-2018学年度第一学期期末八年级数学试卷 题型:解答题
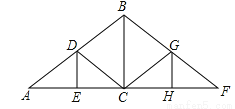
如图是屋架设计图的一部分,其中∠A=30°,点D是斜梁AB的中点,BC、DE垂直于横梁AC,AB=8cm,则立柱BC,DE要多长?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com