
��ͼ������������A��B��C��D�ĸ������㣨���������ʾ����������2AB=BC=3CD����A��D�����ʾ�����ķֱ�Ϊ-5��6����ô�������ϵ�C��ʾ��������____��
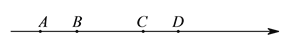

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ���Ϻ��к����2017ѧ����꼶��һѧ�����ս�ѧ������ز��� ���ͣ������
���������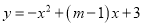 �����㣨2��1������ôm��ֵΪ_____��
�����㣨2��1������ôm��ֵΪ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��������ʡ��������2017-2018ѧ����꼶��ѧ����ĩ������ѧ�Ծ� ���ͣ������
��ʽ����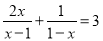 �Ľ���_____.
�Ľ���_____.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ������У2017-2018ѧ�����꼶��ѧ����ĩ������ѧ�Ծ� ���ͣ������
��̽����֪��
��ͼ1������OC�ڡ�AOB���ڲ���ͼ�й���3���ǣ���AOB����AOC�͡�BOC����������һ���ǵĶ�������һ���Ƕ������������������OC�ǡ�AOB�ġ�����ߡ���
��������⡿
��1����ͼ2������MPN= 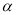 ��������PQ�ǡ�MPN�ġ�����ߡ������NPQ= ____ �����ú�
��������PQ�ǡ�MPN�ġ�����ߡ������NPQ= ____ �����ú�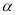 �Ĵ���ʽ��ʾ�����п��ܵĽ����
�Ĵ���ʽ��ʾ�����п��ܵĽ����
���������
��ͼ2������MPN=54�㣬������PQ�Ƶ�P��PNλ�ÿ�ʼ����ÿ��8����ٶ�˳ʱ����ת����PQ��PN��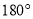 ʱֹͣ��ת����ת��ʱ��Ϊt�룮
ʱֹͣ��ת����ת��ʱ��Ϊt�룮
��2����tΪ��ֵʱ������PM�ǡ�QPN�ġ�����ߡ���
��3��������PMͬʱ�Ƶ�P��ÿ��6����ٶ�˳ʱ����ת������PQͬʱֹͣ�������������PQ �ǡ�MPN�ġ�����ߡ�ʱt��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ������У2017-2018ѧ�����꼶��ѧ����ĩ������ѧ�Ծ� ���ͣ������
�ⷽ�̣��飩��
��1�� ��2��
��2�� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ������У2017-2018ѧ�����꼶��ѧ����ĩ������ѧ�Ծ� ���ͣ������
������ͼ��ʾ�IJ������裬�������ֵΪ��3����ô����Ľ����________��
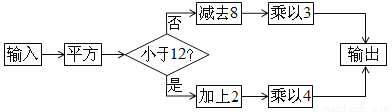
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ������У2017-2018ѧ�����꼶��ѧ����ĩ������ѧ�Ծ� ���ͣ���ѡ��
����ͼ�仯������ȷ���ǣ� ����
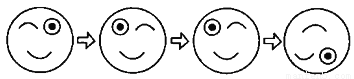
A. ƽ�ơ����ۡ���ת B. ƽ�ơ���ת������
C. ���ۡ�ƽ�ơ���ת D. ���ۡ���ת��ƽ��
C ���������������� ��һ��ͼ�䵽�ڶ���ͼ�Ƿ��ۣ��ڶ���ͼ�䵽������ͼ��ƽ�ƣ�������ͼ�䵽���ĸ�ͼ����ת����ѡC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㽭���ݸ���2016-2017ѧ����꼶��ѧ����ĩ��ѧ�Ծ� ���ͣ���ѡ��
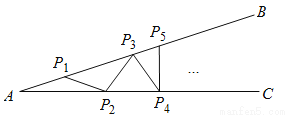
��ͼ��ʾ���ӹ̸ּ�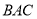 �����ֻ�ܺ���
�����ֻ�ܺ���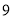 ���ȳ��ĸ�����
���ȳ��ĸ����� 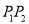 ��
�� 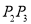 ��
��  ��
�� 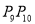 ����
����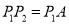 ����
����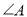 ��ȡֵ��Χ�ǣ�������
��ȡֵ��Χ�ǣ�������
A. 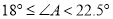 B.
B. 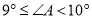
C. 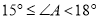 D.
D. 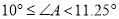
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ����ʦ�����꼶��ѧ�ϲ� ������ ƽ���ߵ�֤�� ��Ԫ���� ���ͣ������
��ͼ����֪��ABC=52�㣬��ACB=60�㣬BO��CO�ֱ��ǡ�ABC�͡�ACB��ƽ���ߣ�EF����O����ƽ����BC�����BOC�Ķ�����
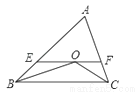
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com