
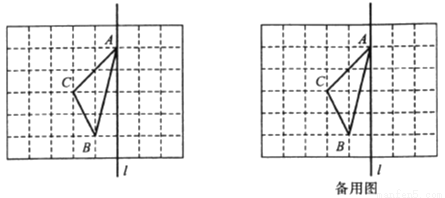
如图,在长度为1个单位长度的小正方形组成的正方形网格中, 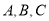 在小正方形的顶点上.
在小正方形的顶点上.
(1)在图中画出与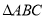 关于直线l成轴对称的
关于直线l成轴对称的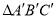 .
.
(2)在直线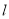 上找一点
上找一点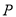 (在备用图中标出),使
(在备用图中标出),使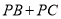 的长最短,这个最短长度的平方值是 .
的长最短,这个最短长度的平方值是 .
科目:初中数学 来源:2017年广西南宁市兴宁区英华学校中考数学模拟试卷 题型:单选题
已知一条抛物线经过E(0,10),F(2,2),G(4,2),H(3,1)四点,选择其中两点用待定系数法能求出抛物线解析式的为( )
A. E,F B. E,G C. E,H D. F,G
C 【解析】试题解析: ∵F(2,2),G(4,2), ∴F和G点为抛物线上的对称点, ∴抛物线的对称轴为直线x=3, ∴H(3,1)点为抛物线的顶点, 设抛物线的解析式为 把E(0,10)代入得9a+1=10,解得a=1, ∴抛物线的解析式为 故选C.查看答案和解析>>
科目:初中数学 来源:福建省三明市大田县2017-2018学年八年级上期末模拟数学试卷 题型:解答题
如图,在△ACB中,∠ACB=90゜,CD⊥AB于D.
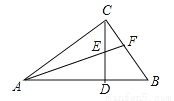
(1)求证:∠ACD=∠B;
(2)若AF平分∠CAB分别交CD、BC于E、F,求证:∠CEF=∠CFE.
(1)证明见解析;(2)证明见解析. 【解析】 试题分析:(1)由于∠ACD与∠B都是∠BCD的余角,根据同角的余角相等即可得证; (2)根据直角三角形两锐角互余得出∠CFA=90°-∠CAF,∠AED=90°-∠DAE,再根据角平分线的定义得出∠CAF=∠DAE,然后由对顶角相等的性质,等量代换即可证明∠CEF=∠CFE. 试题解析:(1)∵∠ACB=90゜,CD⊥AB于...查看答案和解析>>
科目:初中数学 来源:福建省三明市大田县2017-2018学年八年级上期末模拟数学试卷 题型:单选题
小明有两根3cm、7cm的木棒,他想以这两根木棒为边做一个三角形,还需再选用的木棒长可以为( )
A. 3cm B. 4cm C. 9cm D. 10cm
C 【解析】试题分析:由题意可知,A项,3+3<7,故不符合题意;B项,3+4=7,故不符合题意;D项,3+7=10,故不符合题意;C项,3+9>7,符合题意,故选C项.查看答案和解析>>
科目:初中数学 来源:2017-2018学年苏州市第一学期八年级数学期末复习综合检测卷 题型:解答题
如图,等边三角形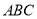 的边长为4,点
的边长为4,点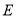 是边
是边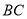 上一动点(不与点
上一动点(不与点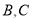 重合),以
重合),以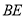 为边在
为边在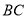 的下方作等边三角形
的下方作等边三角形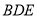 ,连接
,连接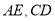 .
.
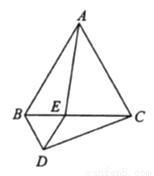
(1)在运动的过程中, 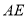 与
与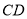 有何数量关系?请说明理由.
有何数量关系?请说明理由.
(2)当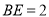 时,求
时,求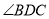 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年苏州市第一学期八年级数学期末复习综合检测卷 题型:填空题
一个等腰三角形的一个角为80°,则它的顶角的度数是_________.
80°或20° 【解析】试题解析:(1)当80°角为顶角,顶角度数即为80°; (2)当80°为底角时,顶角=180°-2×80°=20°. 故答案为:80°或20°.查看答案和解析>>
科目:初中数学 来源:2017-2018学年苏州市第一学期八年级数学期末复习综合检测卷 题型:单选题
一等腰三角形底边长为8 cm,腰长为5 cm,则腰上的高为( )
A. 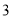 cm B.
cm B. 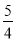 cm C.
cm C. 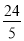 cm D.
cm D. 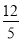 cm
cm
查看答案和解析>>
科目:初中数学 来源:山东省2017-2018学年八年级上学期第二次月考数学试卷 题型:填空题
“同角的余角相等”的题设是__________________,结论是____________________.
如果是同角的余角;那么这两个角相等. 【解析】试题分析:命题一般都能够写成“如果…,那么…”的形式,“如果”后面就是题设,“那么”后面就是结论,因此可正确找出题设和结论. 试题解析:“同角的余角相等”可写成是“如果是同角的余角,那么这两个角相等”.查看答案和解析>>
科目:初中数学 来源:2017年甘肃省白银市中考数学二模试卷 题型:解答题
有A、B两个黑布袋,A布袋中有四个除标号外完全相同的小球,小球上分别标有数字1,2,3,4,B布袋中有三个除标号外完全相同的小球,小球上分别标有数字2,4,6.小明先从A布袋中随机取出﹣个小球,用m表示取出的球上标有的数字,再从B布袋中随机取出一个小球,用n表示取出的球上标有的数字.
(1)若用(m,n)表示小明取球时m与n 的对应值,请画出树形图或列表写出(m,n)的所有取值;
(2)求关于x的一元二次方程x2﹣mx+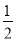 n=0有实数根的概率.
n=0有实数根的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com