练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    已知一条抛物线经过E（0，10），F（2，2），G（4，2），H（3，1）四点，选择其中两点用待定系数法能求出抛物线解析式的为（　　）

    A. E，F B. E，G C. E，H D. F，G

    C 【解析】试题解析： ∵F(2,2),G(4,2)， ∴F和G点为抛物线上的对称点， ∴抛物线的对称轴为直线x=3， ∴H(3,1)点为抛物线的顶点， 设抛物线的解析式为 把E(0,10)代入得9a+1=10，解得a=1， ∴抛物线的解析式为 故选C.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：浙江省宁波市2017-2018学年七年级上册期末模拟数学试卷 题型：单选题

    下列各组数中，互为相反数的有（　　）

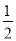    ①2和；②-2和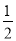；③2.25和?2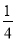；④+（-2）和（-2）；⑤-2和-（-2）；⑥+（+5）和-（-5）

    A. 2组 B. 3组 C. 4组 D. 5组

    A 【解析】根据只有符号不同的两个数互为相反数，可得：③2.25和?2；⑤-2和-（-2)互为相反数， 故选：A．

    查看答案和解析>>

    科目：初中数学 来源：甘肃省张掖市2017-2018学年七年级（上）期中数学试卷 题型：填空题

    截至2013年3月底，某市人口总数已达到4 230 000人．将4 230 000用科学记数法表示为_____．

    4.23×106 【解析】根据科学记数法的书写规则， ，a中的整数部分仅含有一位，n是原数的整数位数减1，易得4 230 000=4.23×106

    查看答案和解析>>

    科目：初中数学 来源：2017年广西南宁市兴宁区英华学校中考数学模拟试卷 题型：解答题

    如图，直线AB分别交y轴、x轴于A、B两点，OA=2，tan∠ABO=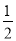，抛物线y=﹣x2+bx+c过A、B两点．

    （1）求直线AB和这个抛物线的解析式；

    （2）设抛物线的顶点为D，求△ABD的面积；

    （3）作垂直x轴的直线x=t，在第一象限交直线AB于M，交这个抛物线于N．求当t取何值时，MN的长度l有最大值？最大值是多少？

    （1）y=﹣x+2；（2） （3）当t=2时，MN的长度l有最大值，最大值是4． 【解析】（1）∵在Rt△AOB中，tan∠ABO=，OA=2，即=， ∴0B=4，∴A（0，2），B（4，0）， 把A、B的坐标代入y=﹣x2+bx+c得： ，解得：b=， ∴抛物线的解析式为y=﹣x2+x+2， 设直线AB的解析式为y=kx+e，把A、B的坐标代入得： ， 解得：...

    查看答案和解析>>

    科目：初中数学 来源：2017年广西南宁市兴宁区英华学校中考数学模拟试卷 题型：填空题

    有一列数﹣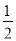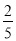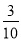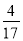， ，﹣， ，…那么第9个数是_____．

    - 【解析】试题解析：∵第n个数为 ∴第9个数是 故答案为：

    查看答案和解析>>

    科目：初中数学 来源：2017年广西南宁市兴宁区英华学校中考数学模拟试卷 题型：单选题

    下列运算正确的是（ ）

    A．（a5）2=a10 B．x16÷x4=x4 C．2a2+3a2=5a4 D．b3•b3=2b3

    A 【解析】 试题分析：根据幂的乘方底数不变指数相乘，同底数幂的除法底数不变指数相减，合并同类项系数相加字母及指数不变，同底数幂的乘法底数不变指数相加，可得答案．A、幂的乘方底数不变指数相乘，故A正确； B、同底数幂的除法底数不变指数相减，故B错误；C、合并同类项系数相加字母及指数不变，故C错误； D、同底数幂的乘法底数不变指数相加，故D错误；

    查看答案和解析>>

    科目：初中数学 来源：浙江省2017-2018学年八年级12月月考数学试卷 题型：解答题

    如图，直线y=-2x+6与坐标轴分别交于点A,B，正比例函数y=x的图象与直线y=-2x+6交于点C。

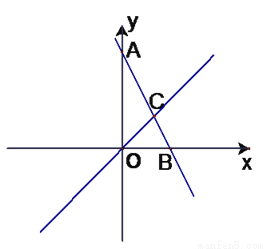
    （1）求点A、B的坐标。

    （2）求△BOC的面积

    （3）已知点P是y轴上的一个动点，求BP+CP的最小值和此时点P的坐标。

    （1）A(0，6) ,B(3，0)；（2）3；（4）,（0， ）. 【解析】试题分析：令直线y=-2x+6中x、y分别为0，即可求得点A、B坐标； （2）先了联立方程组，解得点C的坐标，再由三角形面积公式求得△BOC的面积； （3）作点C关于y轴对称点，连接B,与y轴交点即为使BP+CP取得最小值的点P的坐标. 试题解析：（1）令x=0,得y=6，令y=0，得x=3， ...

    查看答案和解析>>

    科目：初中数学 来源：浙江省2017-2018学年八年级12月月考数学试卷 题型：单选题

    若不等式组的解为，则m的取值范围是（ ）

    A. B. C. D.

    A 【解析】， 由①得：x<8， 由②得：x

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年苏州市第一学期八年级数学期末复习综合检测卷 题型：解答题

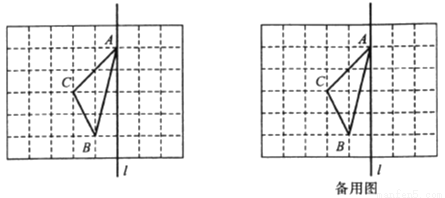
    如图，在长度为1个单位长度的小正方形组成的正方形网格中， 在小正方形的顶点上.

    (1)在图中画出与关于直线l成轴对称的.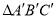

    (2)在直线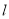上找一点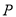 (在备用图中标出)，使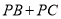的长最短，这个最短长度的平方值是 .

    (1)作图见解析；(2) 13. 【解析】试题分析：（1）分别找到各点的对称点，顺次连接可得△A′B′C′． （2）连接B'C，则B'C与l的交点即是点P的位置，求出PB+PC的值即可． 试题解析：（1）如图所示： ． （2）如图所示： PB+PC=PB'+PC=B'C=． 则这个最短长度的平方值是13．

    查看答案和解析>>

    同步练习册答案