练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    下列各式从左到右的变形中，是因式分解的为（ ）

    A. x2-1=(x+1)(x-1) B. x2-1+y2=(x+1)(x-1) +y2

    C. x(a-b)=ax-bx D. ax+bx+c=x(a+b)+c

    A 【解析】由因式分解的概念可以判断是因式分解的为A选项. 故选A.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：北京市顺义区2018届初三上学期期末考试数学试卷 题型：填空题

    在平面直角坐标系xOy中，抛物线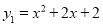可以看作是抛物线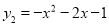经过若干次图形的变化（平移、翻折、旋转）得到的，写出一种由抛物线y2得到抛物线y1的过程：__________．

    抛物线y2先绕点（-1，0）旋转180°，然后再向上平移1个单位长度即可得到抛物线y1（答案不唯一） 【解析】=（x+1）2+1， =-（x+1）2， 抛物线y2先绕点（-1，0）旋转180°，然后再向上平移1个单位长度即可得到抛物线y1， 故答案为：抛物线y2先绕点（-1，0）旋转180°，然后再向上平移1个单位长度即可得到抛物线y1（答案不唯一）.

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年陕西安市九年级（上）期末数学试卷 题型：单选题

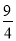    -和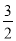（-）2的关系是（ ）

    A. 相等 B. 互为相反数 C. 互为倒数 D. 上述答案都不正确

    B 【解析】根据乘方运算的性质，可知（-）2=，故它们互为相反数. 故选：B.

    查看答案和解析>>

    科目：初中数学 来源：北京市2017-2018学年第一学期八年级数学期中试卷 题型：填空题

    多项式x2﹣8x+k是一个完全平方式，则k=_____．

    16 【解析】k=（－4）2=16. 故答案为16.

    查看答案和解析>>

    科目：初中数学 来源：北京市2017-2018学年第一学期八年级数学期中试卷 题型：单选题

    如图，某同学把一块三角形的玻璃打碎成三片，现在他要到玻璃店去配一块完全一样形状的玻璃，那么最省事的办法是带( )去配

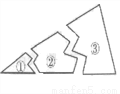
    A. ① B. ② C. ③ D. ①和②

    C 【解析】第③块玻璃有完整的两角及其所夹边，我们可以根据角边角定理配出另一块玻璃与之全等. 故选C.

    查看答案和解析>>

    科目：初中数学 来源：北京市分校2017-2018学年度第一学期期中初二数学试卷 题型：解答题

    在Rt△ABC中,∠ACB=90°,BC=2cm,CD⊥AB，在AC上取一点E，使EC=BC，过点E作EF⊥AC交CD的延长线于点F.若EF=5cm，求AE的长。

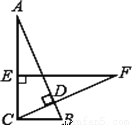
    3cm 【解析】试题分析： 由已知条件易证△ABC≌△FCE，从而可得AC=EF=5，结合EC=BC=2即可得到AE=AC-EC=3. 试题解析： ∵CD⊥AB，EF⊥AC， ∴∠AEF=∠FEC=∠ADF=∠ACB=90o， ∴∠A+∠1=90o，∠F+∠2=90o， 又∵∠1=∠2， ∴∠A=∠F， 在△ABC和△FCE中： ， ∴△...

    查看答案和解析>>

    科目：初中数学 来源：北京市分校2017-2018学年度第一学期期中初二数学试卷 题型：填空题

    小明同学在学习了全等三角形的相关知识后发现，只用两把完全相同的长方形直尺就可以作出一个角的平分线．如图：一把直尺压住射线OB，另一把直尺压住射线OA并且与第一把直尺交于点P，小明说：“射线OP就是∠BOA的角平分线．”他这样做的依据是_____________.

    角的内部到角的两边的距离相等的点在角的平分线上 【解析】如图，由题意可知，PD⊥OB，PE⊥OA，且PD=PE， ∴点P在∠AOB的角平分线上，（角的内部到角两边距离相等的点在角的平分线上） ∴OP平分∠AOB. 故答案为：角的内部到角两边距离相等的点在角的平分线上.

    查看答案和解析>>

    科目：初中数学 来源：福建省2016-2017学年八年级下学期期末考试数学试卷 题型：解答题

    在一条笔直的公路上有、两地，甲从地去地，乙从地去地然后立即原路返回地，返回时的速度是原来的2倍，如图是甲、乙两人离地的距离（千米）和时间（小时）之间的函数图象．

    请根据图象回答下列问题：

    （1）、两地的距离是 千米， ；

    （2）求的坐标，并解释它的实际意义；

    （3）请直接写出当取何值时，甲乙两人相距15千米．

    （1）90,2; （2）P ,点的实际意义是甲、乙分别从A、B两地出发，经过1.2小时相遇，这时离B地的距离为54千米;（3）1或1.4或2.75. 【解析】试题分析: （1）根据函数图象就可以得出A、B两地的距离； （2）根据函数图象反应的时间可以求出甲乙的速度，就可以求出相遇时间，就可以求出乙离B地的距离而得出相遇点P的坐标； （3）由待定系数法求出三段函数的解析式，然后建立...

    查看答案和解析>>

    科目：初中数学 来源：上海市黄浦区2018届九年级上学期期末调研测试数学试卷（WORD版） 题型：填空题

    已知a、b、c满足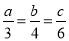，a、b、c都不为0，则=_____．

    【解析】设则所以,故答案为: .

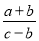    查看答案和解析>>

    同步练习册答案