练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    若关于x的方程2x2﹣ax+a﹣2=0有两个相等的实根，则a的值是_____．

    4 【解析】∵方程有两个相等的实数根， ∴△=（﹣a）2﹣4×2×（a﹣2）=0， 解得a=4， 故答案为：4.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：广东省汕头市潮南区两英镇2018届九年级上学期期末质检数学试卷 题型：单选题

    如图，BD是⊙O的直径，点A、C在⊙O上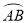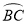，=，∠AOB=60°，则∠BDC的度数是（ ）.

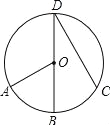
    A．60° B．45° C．35° D．30°

    D． 【解析】 试题分析：直接根据圆周角定理求解．连结OC，如图，∵=，∴∠BDC=∠BOC=∠AOB=×60°=30°． 故选：D．

    查看答案和解析>>

    科目：初中数学 来源：北京市2018届九年级（上）期中数学试卷 题型：填空题

    “服务他人，提升自我”，某学校积极开展家长志愿者服务活动，来自该校初三的5名家长（2男3女）成立了“交通秩序维护”小分队，若从该小分队中任选两名家长进行交通秩序维护，则恰好是一男一女的概率是_____．

    【解析】由题意画树状图如下： 由树形图可知，共有20种等可能的结果，选取的两名家长恰好是一男一女的有12种情况． ∴选取的两名家长恰好是一男一女的概率为： . 故答案为： ．

    查看答案和解析>>

    科目：初中数学 来源：辽宁省大连市沙河口区孙家沟九年制学校2018届九年级（上）期中数学试卷 题型：解答题

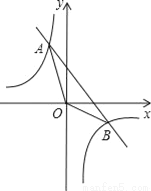
    如图所示，一次函数y=kx+b的图象与反比例函数y=﹣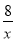的图象交于A、B两点，且点A的横坐标和点B的纵坐标都是﹣2，

    （1）求一次函数的解析式；

    （2）求△AOB的面积．

    （3）直接写出kx+b+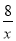＞0的解集．

    （1）y=﹣x+2；（2）6；（3）由函数图象可得当x＜﹣2或0＜x＜4时，kx+b+＞0． 【解析】试题分析：（1）先求出A，B两点坐标，将其代入一次函数关系式即可； （2）根据一次函数与y轴的交点为（0，2），则△AOC和△BOC的底边长为2，两三角形的高分别为|x1|和|x2|，从而可求得其面积； （3）由函数图象得出直线在双曲线上方时x的取值范围． 试题解析：（1）...

    查看答案和解析>>

    科目：初中数学 来源：辽宁省大连市沙河口区孙家沟九年制学校2018届九年级（上）期中数学试卷 题型：填空题

    已知点A（1，a）、点B（b，2）关于原点对称，则a+b的值为_____．

    -3 【解析】∵点A（1，a）、点B（b，2）关于原点对称， ∴b=﹣1，a=﹣2， ∴a+b=﹣3， 故答案为：﹣3．

    查看答案和解析>>

    科目：初中数学 来源：辽宁省大连市沙河口区孙家沟九年制学校2018届九年级（上）期中数学试卷 题型：单选题

    如果代数式x2+4x+4的值是16，则x的值一定是（ ）

    A．-2 B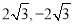． C．2，-6 D．30，-34

    C 【解析】试题分析： 由原题可列方程x2+4x+4=16， ∴x2+4x-12=0， ∴（x-2）（x+6）=0， ∴x=2或x=-6，故本题选C.

    查看答案和解析>>

    科目：初中数学 来源：河南省郑州市郑东新区实验学校2017-2018学年八年级（上）期中数学试卷 题型：解答题

    如图，在锐角三角形ABC中，BC=4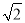，∠ABC=45°，BD平分∠ABC，M、N分别是BD、BC上的动点，试求CM+MN的最小值．

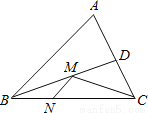
    CM+MN的最小值为4． 【解析】试题分析：过点C作CE⊥AB于点E，交BD于点M′，过点M′作M′N′⊥BC于N′，则CE即为CM+MN的最小值，再根据∠ABC=45°，CE⊥AB，可知△BCE是等腰直角三角形，由锐角三角函数的定义即可求出CE的长． 试题解析： 过点C作CE⊥AB于点E，交BD于点M′，过点M′作M′N′⊥BC于N′，则CE即为CM+MN的最小值， ∵B...

    查看答案和解析>>

    科目：初中数学 来源：河南省郑州市郑东新区实验学校2017-2018学年八年级（上）期中数学试卷 题型：单选题

    点P（x，y）在第四象限，且|x|=3，|y|=2，则P点的坐标是（　　）

    A. （3，2） B. （3，﹣2） C. （﹣2，3） D. （2，﹣3）

    B 【解析】∵点P（x，y）在第四象限，且|x|=3，|y|=2， ∴x=3，y=﹣2， ∴点P的坐标为（3，﹣2）． 故选B．

    查看答案和解析>>

    科目：初中数学 来源：数学人教版八年级上册第11章第二节与三角形有关的角第三课时同步练习 题型：填空题

    如图所示，直线a∥b，∠1=130°，∠2=70°，求则∠3的度数．

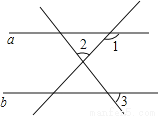
    70° 【解析】试题分析：先根据三角形的外角的性质求得∠4的度数，再根据平行线的性质求解即可. ∵∠1＝130°，∠2＝70° ∴∠4＝130°-70°＝60° ∵a//b ∴∠3＝∠4＝60°.

    查看答案和解析>>

    同步练习册答案