
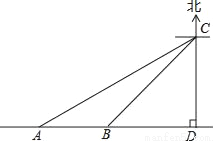
据调查,超速行驶是引发交通事故的主要原因之一.上周末,小明和三位同学用所学过的知识在一条笔直的道路上检测车速.如图,观测点C到公路的距离CD为100米,检测路段的起点A位于点C的南偏西60°方向上,终点B位于点C的南偏西45°方向上.某时段,一辆轿车由西向东匀速行驶,测得此车由A处行驶到B处的时间为4秒.问此车是否超过了该路段16米/秒的限制速度?(参考数据: 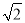 ≈1.4,
≈1.4, 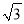 ≈1.7)
≈1.7)
科目:初中数学 来源:2017年天津市中考数学模拟试卷 题型:填空题
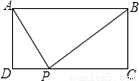
如图,矩形ABCD中,AD=2,AB=5,P为CD边上的动点,当△ADP与△BCP相似时,DP=__.
查看答案和解析>>
科目:初中数学 来源:四川外语学院重庆第二外国语学校2017-2018学年七年级上学期期中考试数学试卷 题型:解答题
化简求值
(1)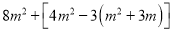 ,其中m=
,其中m=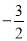
(2)已知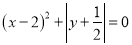 ,求代数式
,求代数式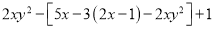 的值
的值
查看答案和解析>>
科目:初中数学 来源:四川外语学院重庆第二外国语学校2017-2018学年七年级上学期期中考试数学试卷 题型:单选题
有人用
A. 收支平衡 B. 赚了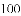
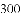
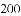
查看答案和解析>>
科目:初中数学 来源:四川外语学院重庆第二外国语学校2017-2018学年七年级上学期期中考试数学试卷 题型:单选题
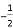 的倒数是( )
的倒数是( )
A.  B. -2 C. 2 D.
B. -2 C. 2 D. 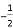
查看答案和解析>>
科目:初中数学 来源:2017年安徽省中考数学模拟试卷 题型:填空题
如图,一束光线从点A(3,3)出发,经过y轴上点C反射后经过点B(1,0),则光线从点A到点B经过的路径长为_____.
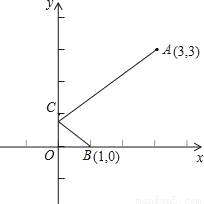
查看答案和解析>>
科目:初中数学 来源:2017年安徽省中考数学模拟试卷 题型:单选题
若关于x,y的多项式0.4x2y﹣7mxy+0.75y3+6xy化简后不含二次项,则m=( )
A. 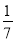 B.
B. 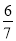 C. ﹣
C. ﹣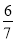 D. 0
D. 0
查看答案和解析>>
科目:初中数学 来源:湖南省2018届九年级数学上期末复习检测数学试卷 题型:解答题
下表给出了代数式﹣x2+bx+c与x的一些对应值:
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | … |
﹣x2+bx+c | … | 5 | n | c | 2 | ﹣3 | ﹣10 | … |
(1)根据表格中的数据,确定b,c,n的值;
(2)设y=﹣x2+bx+c,直接写出0≤x≤2时y的最大值.
(1)b=-2,c=5,n=6;(2)y的最大值是5. 【解析】试题分析:(1)把(﹣2,0)、(1,2)分别代入﹣x2+bx+c中得到关于b、c的方程组,然后解方程组即可得到b、c的值;然后计算x=﹣1时的代数式的值即可得到n的值; (2)利用表中数据即可求解. 试题解析:(1)根据表格数据可得 ,解得, ∴﹣x2+bx+c=﹣x2﹣2x+5, 当x=﹣1时,﹣x2...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com