
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:福建省泉州市2017-2018学年七年级下期末质量检测数学试卷 题型:解答题
阅读下列材料:
我们知道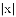 的几何意义是在数轴上数
的几何意义是在数轴上数
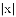 =
=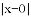 ,也就是说,
,也就是说,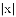 表示在数轴上数
表示在数轴上数
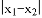 表示在数轴上数
表示在数轴上数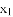 与数
与数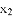 对应的点之间的距离;
对应的点之间的距离;
例1.解方程|
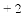

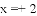
例2.解不等式|








例3.解方程|











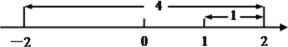
参考阅读材料,解答下列问题:
(1)方程|
(2)解不等式:|
(3)解不等式:|

查看答案和解析>>
科目:初中数学 来源:贵州省铜仁市2018年中考数学试卷 题型:单选题
在同一平面内,设a、b、c是三条互相平行的直线,已知a与b的距离为4cm,b与c的距离为1cm,则a与c的距离为( )
A. 1cm B. 3cm C. 5cm或3cm D. 1cm或3cm
查看答案和解析>>
科目:初中数学 来源:安徽省毕业考试模拟冲刺数学卷(四) 题型:填空题
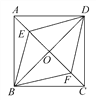
如图,已知正方形ABCD的对角线交于O点,点E,F分别是AO,CO的中点,连接BE,BF,DE,DF,则下列结论中一定成立的是________.(把所有正确结论的序号都填在横线上)
①BF=DE;②∠ABO=2∠ABE;③S△AED=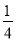 S△ACD;④四边形BFDE是菱形.
S△ACD;④四边形BFDE是菱形.
查看答案和解析>>
科目:初中数学 来源:安徽省毕业考试模拟冲刺数学卷(四) 题型:单选题
(2013年四川自贡4分)如图,点O是正六边形的对称中心,如果用一副三角板的角,借助点O(使该角的顶点落在点O处),把这个正六边形的面积n等分,那么n的所有可能取值的个数是( )
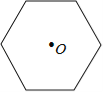
A. 4 B. 5 C. 6 D. 7
查看答案和解析>>
科目:初中数学 来源:湖南省2018届九年级中考数学模拟试卷 题型:解答题
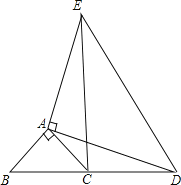
如图,△ABC和△ADE都是等腰三角形,且∠BAC=90°,∠DAE=90°,B,C,D
在同一条直线上.求证:BD=CE.
查看答案和解析>>
科目:初中数学 来源:北京市2017-2018学年第二学期数学期中试卷 题型:解答题
在《九章算术》中有求三角形面积公式“底乘高的一半”,但是在实际丈量土地面积时,量出高并非易事,所以古人想到了能否利用三角形的三条边长来求面积.我国南宋著名的数学家秦九韶(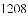
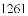
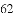
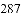
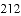
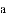
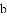
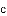
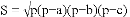 (公式里的
(公式里的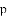
请利用海伦一秦九韶公式解决以下问题:
(
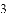
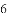
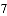
(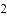
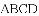
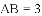
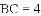
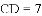
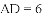
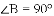
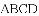
(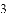
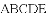
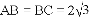 ,
,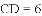
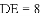
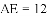
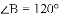
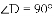
查看答案和解析>>
科目:初中数学 来源:江西省九江市2017-2018学年度七年级下学期期末考试数学试卷 题型:填空题
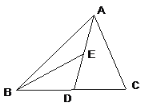
如图△ABC中,AD是BC上的中线,BE是△ABD中AD边上的中线,若△ABC的面积是24,则△ABE的面积是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com