
在一块平地上,张大爷家屋前9米远处有一颗大树,在一次强风中,这课大树从离地面6米处折断倒下,量得倒下部分的长是10米,大树倒下时能砸到张大爷的房子吗?( )

A.一定不会 B.可能会
C.一定会 D.以上答案都不对
A 【解析】【解析】 如图所示,AB=10米,AC=6米,根据勾股定理得, BC===8米<9米. 故选:A.科目:初中数学 来源:黄金30题系列 九年级数学 小题好拿分 题型:单选题
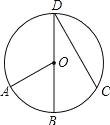
如图,BD是⊙O的直径,点A、C在⊙O上,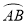 =
=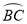 ,∠AOB=60°,则∠BDC的度数是( ).
,∠AOB=60°,则∠BDC的度数是( ).
A.60° B.45° C.35° D.30°
D. 【解析】 试题分析:直接根据圆周角定理求解.连结OC,如图,∵=,∴∠BDC=∠BOC=∠AOB=×60°=30°. 故选:D.查看答案和解析>>
科目:初中数学 来源:2017年广东省东莞市堂星晨学校考数学模拟试卷 题型:单选题
如图为二次函数y=ax2+bx+c (a≠0)的图象,则下列说法:①a>0 ②2a+b=0 ③a+b+c>0 ④ 当-1<x<3时,y>0 其中正确的个数为()
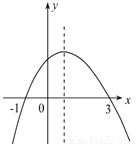
A. 1 B. 2 C. 3 D. 4
C 【解析】试题分析:①由二次函数y=ax2+bx+c(a≠0)的开口向下,可知a<0,故错误; ②由二次函数与x轴的交点的坐标为(-1,0),(3,0),可知对称轴为x==1,即-=1, 因此可得b=-2a,即2a+b=0,故正确; ③由函数的顶点在第一象限,因此可知,当x=1时,y=a+b+c>0,故正确; ④由二次函数与x轴的交点的坐标为(-1,0),(3,0)...查看答案和解析>>
科目:初中数学 来源:2018年春人教版八年级数学下册(广西)期中测试 题型:填空题
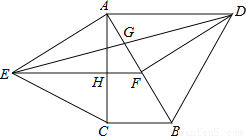
如图,分别以直角△ABC的斜边AB,直角边AC为边向△ABC外作等边△ABD和等边△ACE,F为AB的中点,DE与AB交于点G,EF与AC交于点H,∠ACB=90°,∠BAC=30°.给出如下结论:
①EF⊥AC;②四边形ADFE为菱形;③AD=4AG;④FH=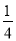 BD
BD
其中正确结论的为______(请将所有正确的序号都填上).
查看答案和解析>>
科目:初中数学 来源:2018年春人教版八年级数学下册(广西)期中测试 题型:单选题
如图,矩形ABCD的边长AB=6,BC=8,将矩形沿EF折叠,使点C与点A重合,则折痕EF的长是( )
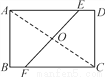
A. 7.5 B. 6 C. 10 D. 5
A 【解析】试题分析:根据矩形的性质可得AC=10,根据折叠图形可得AE=FC=AF,AO=CO=5,然后设AE=x,则BF=8-x,根据直角△ABF的勾股定理求出x的值,然后计算EF的长度.查看答案和解析>>
科目:初中数学 来源:2018年春人教版八年级数学下册(广西)期中测试 题型:单选题
若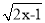 在实数范围内有意义,则x的取值范围是( )
在实数范围内有意义,则x的取值范围是( )
A. x≥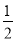 B. x≥-
B. x≥-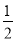 C. x>
C. x>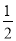 D. x≠
D. x≠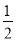
查看答案和解析>>
科目:初中数学 来源:黄金30题系列 九年级数学 小题好拿分 题型:单选题
如图所示,CD为⊙O的直径,弦AB⊥CD,垂足为E,AB=10,CE =1,则直径CD的长为( )

A.16 B.24 C.36 D.26
D 【解析】 试题分析:连接AO,设AO=r,根据垂径定理可得:AE=5,OE=r-1,根据Rt△AOE的勾股定理可得:r=13,则CD=2r=26.查看答案和解析>>
科目:初中数学 来源:青海省2017-2018学年七年级上学期12月月考数学试卷 题型:填空题
若2a﹣b=3,则多项式8a﹣4b+3的值是______.
15 【解析】试题解析: 故答案为:查看答案和解析>>
科目:初中数学 来源:江苏省东台市第三教育联盟2017-2018学年度第一学期第三次阶段检测七年级数学试卷 题型:解答题
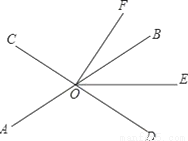
如图,直线AB、CD相交于点O,OE平分∠BOD.
(1)若∠AOC=70°,∠DOF=90°,求∠EOF的度数;
(2)若OF平分∠COE,∠BOF=15°,若设∠AOE=x°.
①用含x的代数式表示∠EOF;
②求∠AOC的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com