
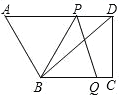
如图,在四边形ABCD中,AD//BC, 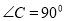 ,BC=4,DC=3,AD=6.动点P从点D出发,沿射线DA的方向,在射线DA上以每秒2两个单位长的速度运动,动点Q从点C出发,在线段CB上以每秒1个单位长的速度向点B运动,点P、Q分别从点D,C同时出发,当点Q运动到点B时,点P随之停止运动.设运动的时间为t(秒).
,BC=4,DC=3,AD=6.动点P从点D出发,沿射线DA的方向,在射线DA上以每秒2两个单位长的速度运动,动点Q从点C出发,在线段CB上以每秒1个单位长的速度向点B运动,点P、Q分别从点D,C同时出发,当点Q运动到点B时,点P随之停止运动.设运动的时间为t(秒).
(1)设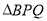 的面积为
的面积为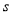 ,直接写出
,直接写出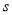 与
与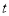 之间的函数关系式是____________(不写取值范围).
之间的函数关系式是____________(不写取值范围).
(2)当B,P,Q三点为顶点的三角形是等腰三角形时,求出此时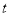 的值.
的值.
(3)当线段PQ与线段AB相交于点O,且2OA=OB时,直接写出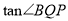 =_____________.
=_____________.
(4)是否存在时刻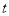 ,使得
,使得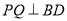 若存在,求出
若存在,求出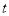 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源:江苏省无锡锡山区锡东片2016-2017学年第二学期4月八年级数学期中试卷 题型:填空题
一个袋中装有6个红球,4个黄球,1个白球,每个球除颜色外都相同,任意摸出一球,摸到____球的可能性最大
查看答案和解析>>
科目:初中数学 来源:2018年吉林省中考数学一模试卷 题型:解答题
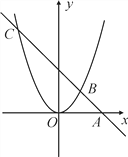
如图,直线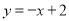 过
过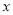 轴上的点A(2,0),且与抛物线
轴上的点A(2,0),且与抛物线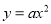 交于B,C两点,点B坐标为(1,1).
交于B,C两点,点B坐标为(1,1).
(1)求抛物线的函数表达式;
(2)连结OC,求出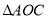 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源:2018年吉林省中考数学一模试卷 题型:填空题
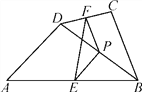
如图,四边形ABCD中,点P是对角线BD的中点,点E,F分别是AB,CD的中点,AD=BC,∠PEF=35°,则∠PFE的度数是 _________°.
查看答案和解析>>
科目:初中数学 来源:沪科版七年级下册数学 第7章一元一次不等式与不等式组 单元检测 题型:填空题
某校组织开展了“吸烟有害健康”的知识竞赛,共有20道题.答对一题加10分,答错(或不答)一题扣5分,小明参加本次竞赛得分要不低于140分.设他答对x道题,则根据题意,可列出关于x的不等式为________.
查看答案和解析>>
科目:初中数学 来源:2018年湖北省武汉市中考数学一模试卷 题型:解答题
阅读下列材料,完成任务:
自相似图形
定义:若某个图形可分割为若干个都与它相似的图形,则称这个图形是自相似图形.例如:正方形ABCD中,点E、F、G、H分别是AB、BC、CD、DA边的中点,连接EG,HF交于点O,易知分割成的四个四边形AEOH、EBFO、OFCG、HOGD均为正方形,且与原正方形相似,故正方形是自相似图形.
任务:
(1)图1中正方形ABCD分割成的四个小正方形中,每个正方形与原正方形的相似比为 ;
(2)如图2,已知△ABC中,∠ACB=90°,AC=4,BC=3,小明发现△ABC也是“自相似图形”,他的思路是:过点C作CD⊥AB于点D,则CD将△ABC分割成2个与它自己相似的小直角三角形.已知△ACD∽△ABC,则△ACD与△ABC的相似比为 ;
(3)现有一个矩形ABCD是自相似图形,其中长AD=a,宽AB=b(a>b).
请从下列A、B两题中任选一条作答:我选择 题.
A:①如图3﹣1,若将矩形ABCD纵向分割成两个全等矩形,且与原矩形都相似,则a= (用含b的式子表示);
②如图3﹣2若将矩形ABCD纵向分割成n个全等矩形,且与原矩形都相似,则a= (用含n,b的式子表示);
B:①如图4﹣1,若将矩形ABCD先纵向分割出2个全等矩形,再将剩余的部分横向分割成3个全等矩形,且分割得到的矩形与原矩形都相似,则a= (用含b的式子表示);
②如图4﹣2,若将矩形ABCD先纵向分割出m个全等矩形,再将剩余的部分横向分割成n个全等矩形,且分割得到的矩形与原矩形都相似,则a= (用含m,n,b的式子表示).

【答案】(1) ;(2)
;(2) ;(3)A、①
;(3)A、① ;②
;② ;B、①
;B、① 或
或 ;②
;② 或
或 .
.
【解析】试题分析:(1)根据相似比的定义求解即可;(2)由勾股定理求得AB=5,根据相似比等于 可求得答案;(3)A.①由矩形ABEF∽矩形FECD,列出比例式整理可得;②由每个小矩形都是全等的,可得其边长为b和
可求得答案;(3)A.①由矩形ABEF∽矩形FECD,列出比例式整理可得;②由每个小矩形都是全等的,可得其边长为b和 a,列出比例式整理即可;B.①分当FM是矩形DFMN的长时和当DF是矩形DFMN的长时两种情况,根据相似多边形的性质列比例式求解;②由题意可知纵向2块矩形全等,横向3块矩形也全等,所以DN=
a,列出比例式整理即可;B.①分当FM是矩形DFMN的长时和当DF是矩形DFMN的长时两种情况,根据相似多边形的性质列比例式求解;②由题意可知纵向2块矩形全等,横向3块矩形也全等,所以DN= b,然后分当FM是矩形DFMN的长时和当DF是矩形DFMN的长时两种情况,根据相似多边形的性质列比例式求解.
b,然后分当FM是矩形DFMN的长时和当DF是矩形DFMN的长时两种情况,根据相似多边形的性质列比例式求解.
【解析】
(1)∵点H是AD的中点,
∴AH= AD,
AD,
∵正方形AEOH∽正方形ABCD,
∴相似比为: ==
== ;
;
故答案为: ;
;
(2)在Rt△ABC中,AC=4,BC=3,根据勾股定理得,AB=5,
∴△ACD与△ABC相似的相似比为: =
= ,
,
故答案为: ;
;
(3)A、①∵矩形ABEF∽矩形FECD,
∴AF:AB=AB:AD,
即 a:b=b:a,
a:b=b:a,
∴a= b;
b;
故答案为:
②每个小矩形都是全等的,则其边长为b和 a,
a,
则b: a=a:b,
a=a:b,
∴a= b;
b;
故答案为:
B、①如图2,
由①②可知纵向2块矩形全等,横向3块矩形也全等,
∴DN= b,
b,
Ⅰ、当FM是矩形DFMN的长时,
∵矩形FMND∽矩形ABCD,
∴FD:DN=AD:AB,
即FD: b=a:b,
b=a:b,
解得FD= a,
a,
∴AF=a﹣ a=
a= a,
a,
∴AG=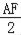 =
= =
= a,
a,
∵矩形GABH∽矩形ABCD,
∴AG:AB=AB:AD
即 a:b=b:a
a:b=b:a
得:a= b;
b;
Ⅱ、当DF是矩形DFMN的长时,
∵矩形DFMN∽矩形ABCD,
∴FD:DN=AB:AD
即FD: b=b:a
b=b:a
解得FD= ,
,
∴AF=a﹣ =
= ,
,
∴AG=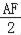 =
= ,
,
∵矩形GABH∽矩形ABCD,
∴AG:AB=AB:AD
即 :b=b:a,
:b=b:a,
得:a= b;
b;
故答案为: 或
或 ;
;
②如图3,
由①②可知纵向m块矩形全等,横向n块矩形也全等,
∴DN= b,
b,
Ⅰ、当FM是矩形DFMN的长时,
∵矩形FMND∽矩形ABCD,
∴FD:DN=AD:AB,
即FD: b=a:b,
b=a:b,
解得FD= a,
a,
∴AF=a﹣ a,
a,
∴AG=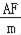 =
= =
= a,
a,
∵矩形GABH∽矩形ABCD,
∴AG:AB=AB:AD
即 a:b=b:a
a:b=b:a
得:a= b;
b;
Ⅱ、当DF是矩形DFMN的长时,
∵矩形DFMN∽矩形ABCD,
∴FD:DN=AB:AD
即FD: b=b:a
b=b:a
解得FD= ,
,
∴AF=a﹣ ,
,
∴AG= =
= ,
,
∵矩形GABH∽矩形ABCD,
∴AG:AB=AB:AD
即 :b=b:a,
:b=b:a,
得:a= b;
b;
故答案为: b或
b或 b.
b.


点睛:本题考查了信息迁移,矩形的性质,相似多边形的性质及分类讨论的数学思想,读懂题意,熟练掌握相似比多边形的性质,正确运用分类讨论思想是解答本题的关键.
【题型】解答题
【结束】
24
如图,在平面直角坐标系xOy中,直线y=kx+b与x轴交于点A,与y轴交于点B.已知抛物线y=﹣x2+bx+c经过A(3,0),B(0,3)两点.
(1)求此抛物线的解析式和直线AB的解析式;
(2)如图①,动点E从O点出发,沿着OA方向以1个单位/秒的速度向终点A匀速运动,同时,动点F从A点出发,沿着AB方向以 个单位/秒的速度向终点B匀速运动,当E,F中任意一点到达终点时另一点也随之停止运动,连接EF,设运动时间为t秒,当t为何值时,△AEF为直角三角形?
个单位/秒的速度向终点B匀速运动,当E,F中任意一点到达终点时另一点也随之停止运动,连接EF,设运动时间为t秒,当t为何值时,△AEF为直角三角形?
(3)如图②,取一根橡皮筋,两端点分别固定在A,B处,用铅笔拉着这根橡皮筋使笔尖P在直线AB上方的抛物线上移动,动点P与A,B两点构成无数个三角形,在这些三角形中是否存在一个面积最大的三角形?如果存在,求出最大面积,并指出此时点P的坐标;如果不存在,请简要说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com