
�����ж���ȷ���ǣ� ����
A. ��һֱ�DZ���ȵ�����ֱ��������ȫ�� B. б����ȵ���������ֱ��������ȫ��
C. ����ȵ���������������ȫ�� D. ������Ƕ�Ӧ��ȵ�����ֱ��������ȫ��
B ��������Aѡ���У���Ϊһ��ֱ�DZ����ʱ���������ߵĴ�С��ϵ����ȷ�������Բ���ȷ�����������Ƿ�ȫ�ȣ�����A��˵������ Bѡ���У�б����ȵ���������ֱ��������ȫ�ȣ���Ϊ��ʱ��ֱ�DZ�һ����ȣ�����B��˵����ȷ�� Cѡ���У�����ȵ��������������εĶ��Dz�һ����ȣ���˲���ȷ�������ĵ���������ȫ�ȣ�����C��˵������ Dѡ���У�������Ƕ�Ӧ��ȵ�����ֱ�������β�һ��ȫ�ȣ���Ϊ��...
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2018�괺��ʦ������꼶��ѧ�²��ҳ���Ծ�����ĩ���� ���ͣ���ѡ��
���м�����ȷ���� ( )
A. a5��a5��a10 B. a3��a2��a6 C. a7��a��a6 D. (��a3)2����6a6
C ��������A. a5��a5��2a5 ����Aѡ�����B. a3��a2��a5 ����Bѡ�����C. a7��a��a6 ����ȷ��D. (��a3)2��a6����Dѡ����� ��ѡC.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017�����ʡ�п���ѧģ���Ծ� ���ͣ���ѡ��
��ͼ��M��ƽ���ı���ABCD��AB���е㣬CM��BD�ڵ�E����ͼ����Ӱ���ֵ������ƽ���ı���ABCD������ı��ǣ�������
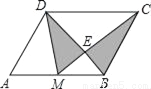
A. 1��3 B. 1��4 C. 1��6 D. 5��12
A ���������������������ͼ����E��GH��CD���ֱ�AB��CD��H��G�� �裬 ��M��AB�е㣬 ���ı���ABCD��ƽ���ı��Σ� ��AB=CD=2a�� ���BME�ס�DCE�� ��EH:GE=BM:CD=1:2�� ��GH=3h�� ��S�ı���ABCD=AB��GH=2a��3h=6ah=12x�� ͬ���� S��Ӱ ��S��Ӱ:S�ı���A...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㽭�����³���������ѧ2017-2018ѧ����꼶��ѧ���п�����ѧ�Ծ����������� ���ͣ������
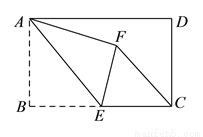
��ͼ���ھ���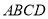 �У�
�� 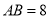 ��
�� 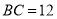 ����
����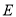 Ϊ
Ϊ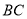 ���е㣬��
���е㣬��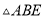 ��
��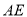 �۵���ʹ��
�۵���ʹ��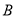 ���ھ����ڵ�
���ھ����ڵ�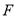 ��������
��������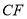 ����
����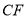 �ij�Ϊ__________��
�ij�Ϊ__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㽭�����³���������ѧ2017-2018ѧ����꼶��ѧ���п�����ѧ�Ծ����������� ���ͣ���ѡ��
����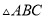 ���ܳ�Ϊ
���ܳ�Ϊ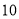 ����������
����������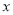 ��ȡֵ��Χ�ǣ� ����
��ȡֵ��Χ�ǣ� ����
A. 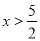 B.
B. 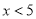 C.
C. 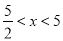 D.
D. 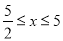
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㽭ʡ����2017-2018ѧ����꼶�ϲ���ĩģ����ѧ�Ծ� ���ͣ������
�������x�IJ���ʽ|x��2|+|x+3|��a����xȡ����������������a��ȡֵ��Χ�Ƕ��٣���˵�����ɣ�
a��5 ����������������������߶��ϵĵ㵽�����˵�ľ���ĺ���С���ɵô𰸣� �����������|x��2|+|x+3|��5�� �����x�IJ���ʽ|x��2|+|x+3|��a����xȡ�������������� a��5���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㽭ʡ����2017-2018ѧ����꼶�ϲ���ĩģ����ѧ�Ծ� ���ͣ������
��ͼ��y=kx+b��ͼ����b= ����x��Ľ�������Ϊ ��y��ֵ��x������� ��
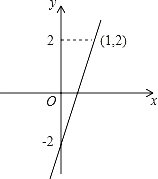
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ������2017-2018ѧ����꼶��ѧ�����п�����ѧ�Ծ� ���ͣ������
��ͼ����ֱ֪��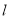 ���O���룬OA��
���O���룬OA��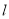 �ڵ�A,����O�ڵ�P,��B�ǡ�O��һ��,����BP���ӳ�,��ֱ��
�ڵ�A,����O�ڵ�P,��B�ǡ�O��һ��,����BP���ӳ�,��ֱ��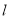 �ڵ�C,ʹ��AB=AC.
�ڵ�C,ʹ��AB=AC.
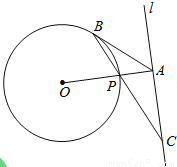
��1����֤:AB�ǡ�O�����ߣ�
��2����PC=2 ,OA=4,���O�İ뾶.
,OA=4,���O�İ뾶.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ����������У2017-2018ѧ����꼶��ѧ������������ѧ�Ծ� ���ͣ������
��ͼ����ABC�У�AD�Ǹߣ�CE�����ߣ���G��CE���е㣬DG��CE����GΪ���㣮
��1����֤��DC=BE��
��2������AEC=66�㣬���BCE�Ķ�����

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com