
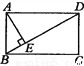
如图所示,矩形ABCD中,AE⊥BD于E,∠DAE=3∠BAE,则∠BAE=_____,∠EAD=_____,∠EAC=_____.
 活力课时同步练习册系列答案
活力课时同步练习册系列答案科目:初中数学 来源:天津市 2017-2018学年 八年级数学上册 全等三角形判定 填空题练习(含答案) 题型:填空题
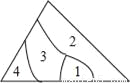
小明将一块三角形的玻璃棒摔碎成如图所示的四块(即图中标有1,2,3,4的四块),若只带一块配成原来一样大小的三角形,则应该带第_______块.
查看答案和解析>>
科目:初中数学 来源:重庆市华东师大版2016-2017学年七年级下学期期中考试数学试卷 题型:解答题
计算:
(1) 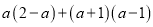 ; (2)
; (2) 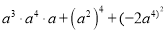
(3) 999.8×1000.2 (用简便方法计算)
(1) 2a-1;(2) 6a8;(3)999999.96. 【解析】试题分析:(1)先计算单项式乘多项式和利用平方差公式计算多项式乘多项式,然后合并同类项即可; (2)分别计算同底数幂的乘法、幂的乘方和积的乘方,然后合并同类项即可; (3)将999.8写成1000-0.2,1000.2写成1000+0.2,然后利用平方差公式计算即可. 试题解析: (1)原式=2a-...查看答案和解析>>
科目:初中数学 来源:重庆市华东师大版2016-2017学年七年级下学期期中考试数学试卷 题型:单选题
计算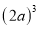 的结果是( )
的结果是( )
A. 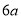 B. 8
B. 8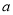 C.
C. 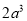 D.
D. 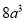
查看答案和解析>>
科目:初中数学 来源:北师大版(2012) 九年级上册同步练习:1.2矩形的性质 题型:解答题
如图,在矩形ABCD中,AC、BD相交于O,AE平分∠BAD,交BC于E,若∠CAE=15°,求∠BOE的度数.
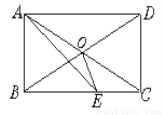
查看答案和解析>>
科目:初中数学 来源:北师大版(2012) 九年级上册同步练习:1.2矩形的性质 题型:填空题
如图所示,O为矩形ABCD的对角线交点,DF平分∠ADC交AC于E,BC于F, ∠BDF=15°,则∠COF=______.
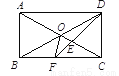
查看答案和解析>>
科目:初中数学 来源:北师大版(2012) 九年级上册同步练习:1.2矩形的性质 题型:单选题
已知E、F分别是矩形ABCD的对边BC和AD上的点,且BE=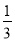 BC,AF=
BC,AF=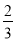 AD,连结AC、EF,那么( ).
AD,连结AC、EF,那么( ).
A. AC平分EF,但EF不平分AC B. AC与EF互相平分
C. EF平分AC,但AC不平分EF D. AC与EF不会互相平分
B 【解析】∵四边形ABCD是矩形,∴AD=BC,AD//BC,∴∠DAC=∠ACB, ∵BE=BC,AF= AD,∴AF=CE, 又∵∠AOF=∠COE,∴△AOF≌△COE, ∴AO=CO,FO=EO,即AC与EF互相平分, 故选B.查看答案和解析>>
科目:初中数学 来源:人教版九年级上册数学 22.1.2二次函数yax2的图象和性质 练习 题型:单选题
下列函数中,具有过原点,且当x>0时,y随x增大而减小,这两个特征的有()
①y=-ax2(a>0) ②y=(a-1)x2(a<1) ③y=-2x+a2(a≠0) ④y=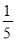 x-a
x-a
A. 1个 B. 2个 C. 3个 D. 4个
B 【解析】(1)∵在①y=-ax2(a>0)中,当x=0是,y=0,且-a<0, ∴其图象过原点,且当x>0时,y随x的增大而减小; (2)∵在② y=(a-1)x2(a<1)中,当x=0时,y=0,且a-1<0, ∴其图象过原点,且当x>0时,y随x的增大而减小; (3)∵在③ y=-2x+a2(a≠0)中,当x=0时,y0, ∴其图象过原点; (4)...查看答案和解析>>
科目:初中数学 来源:人教版八年级上册 第十二章 全等三角形 12.2 三角形全等的判定 同步练习题 含答案 题型:解答题
如图所示,AB=AC,F,E分别是AB,AC的中点.求证:△ABE≌△ACF.
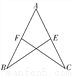
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com