
科目:初中数学 来源:海南省2018届九年级中招模拟考试(三)数学试卷 题型:单选题
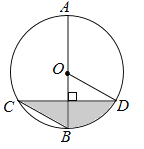
如图,AB是圆O的直径,弦CD⊥AB,∠BCD=30°,CD=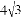 ,则S阴影=( )
,则S阴影=( )
A. 2π B.  π C.
π C.  π D.
π D. 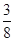 π
π
查看答案和解析>>
科目:初中数学 来源:云南省楚雄州2017-2018学年七年级下学期期末教学质量监测数学试卷 题型:解答题
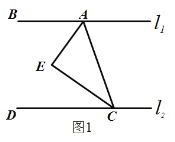
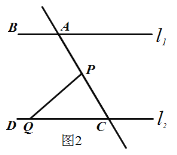
如图1,点A、B在直线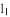 上,点C、D在直线
上,点C、D在直线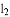 上,AE平分∠BAC,CE平分∠ACD,
上,AE平分∠BAC,CE平分∠ACD,
∠EAC+∠ACE=90° .
(1)请判断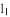 与
与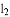 的位置关系并说明理由;
的位置关系并说明理由;
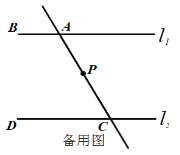
(2)如图2,在(1)的结论下,P为线段AC上一定点,点Q为直线CD上一动点,当点Q在射线CD上运动时(不与点C重合)∠CPQ+∠CQP与∠BAC有何数量关系?请说明理由.
查看答案和解析>>
科目:初中数学 来源:云南省楚雄州2017-2018学年七年级下学期期末教学质量监测数学试卷 题型:单选题
有理数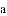
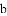
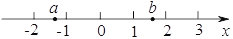
A. 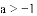
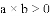
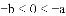
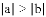
查看答案和解析>>
科目:初中数学 来源:福建省泉州市2017-2018学年七年级下期末质量检测数学试卷 题型:解答题
阅读下列材料:
我们知道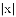 的几何意义是在数轴上数
的几何意义是在数轴上数
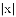 =
=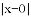 ,也就是说,
,也就是说,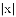 表示在数轴上数
表示在数轴上数
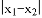 表示在数轴上数
表示在数轴上数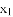 与数
与数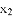 对应的点之间的距离;
对应的点之间的距离;
例1.解方程|
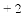

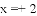
例2.解不等式|








例3.解方程|











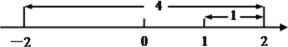
参考阅读材料,解答下列问题:
(1)方程|
(2)解不等式:|
(3)解不等式:|

查看答案和解析>>
科目:初中数学 来源:福建省泉州市2017-2018学年七年级下期末质量检测数学试卷 题型:单选题
在△ABC中,∠A∶∠B∶∠C=1∶2∶3,则△ABC的形状是
A. 等腰三角形 B. 直角三角形 C. 等边三角形 D. 等腰直角三角形
查看答案和解析>>
科目:初中数学 来源:安徽省毕业考试模拟冲刺数学卷(四) 题型:填空题
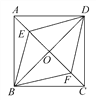
如图,已知正方形ABCD的对角线交于O点,点E,F分别是AO,CO的中点,连接BE,BF,DE,DF,则下列结论中一定成立的是________.(把所有正确结论的序号都填在横线上)
①BF=DE;②∠ABO=2∠ABE;③S△AED=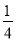 S△ACD;④四边形BFDE是菱形.
S△ACD;④四边形BFDE是菱形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com