
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:浙江杭州西湖区第十三中学2017-2018学年九年级上学期期中考试数学试卷 题型:单选题
下列说法中,正确的是( ).
A. 买一张电影票,座位号一定是奇数
B. 投掷一枚均匀的硬币,正面一定朝上
C. 从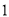 ,
, 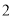 ,
, 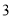 ,
, 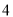 ,
, 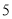 这五个数字中任意取一个数,取得奇数的可能性大
这五个数字中任意取一个数,取得奇数的可能性大
D. 三个点一定可以确定一个圆
C 【解析】A.买一张电影票,座位号不一定是奇数,故本选项错误; B.投掷一枚均匀的硬币,正面不一定朝上,故本选项错误; C.从1、2、3、4、5这五个数字中任意取一个数,取得奇数的可能性是,故本选项正确; D.三条任意长的线段不一定组成一个三角形,故本选项错误; 故选:C.查看答案和解析>>
科目:初中数学 来源:黄金30题系列 九年级数学 小题好拿分 题型:填空题
关于x的方程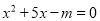 的一个根是-1,则m=______.
的一个根是-1,则m=______.
查看答案和解析>>
科目:初中数学 来源:安徽省芜湖市教育集团2017-2018学年度上学期八年级第二次月考 题型:解答题
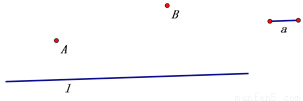
已知A、B两点在直线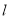 的同侧,试在
的同侧,试在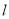 上找两点C和D(CD的长度为定值
上找两点C和D(CD的长度为定值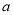 ),使得AC+CD+DB最短(保留作图痕迹,不要求写画法)。
),使得AC+CD+DB最短(保留作图痕迹,不要求写画法)。
查看答案和解析>>
科目:初中数学 来源:安徽省芜湖市教育集团2017-2018学年度上学期八年级第二次月考 题型:填空题
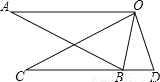
如图,△ABO≌△CDO,点B在CD上,AO∥CD,∠BOD=30°,则∠A=_______°.
查看答案和解析>>
科目:初中数学 来源:安徽省芜湖市教育集团2017-2018学年度上学期八年级第二次月考 题型:单选题
如图,将两根等长钢条AA'、BB'的中点O连在一起,使AA'、BB'可以绕着点O自由转动,就做成了一个测量工件,则AB的长等于容器内径A'B',那么判定△OAB≌△OA′B′的理由是( )
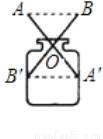
A. 边边边 B. 边角边 C. 角边角 D. 角角边
A. 【解析】 试题分析: ∵O为中点 ∴OA’=OA,OB’=OB ∵AB=A’B’ ∴△OAB≌△OA′B′查看答案和解析>>
科目:初中数学 来源:2017年广东省东莞市堂星晨学校考数学模拟试卷 题型:解答题
如图,AB是⊙O的直径,C是BD的中点,CE⊥AB,垂足为E,BD交CE于点F.

1.求证:CF=BF;
2.若AD=2,⊙O的半径为3,求BC的长
1.连结AC,如图 ∵C是弧BD的中点 ∴∠BDC=∠DBC 又∠BDC=∠BAC 在三角形ABC中,∠ACB=90°,CE⊥AB∴ ∠BCE=∠BAC, ∠BCE=∠DBC ∴ CF=BF 因此,CF=BF. 3分 2.证法一:作CG⊥AD于点G, ∵C是弧BD的中点 ∴∠CAG=∠BAC, 即AC是∠BAD的角平分线. ∴ CE=CG,AE...查看答案和解析>>
科目:初中数学 来源:2017年广东省东莞市堂星晨学校考数学模拟试卷 题型:单选题
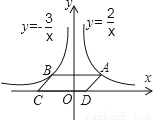
如图,点A是反比例函数y=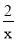 (>0)的图象上任意一点,AB∥x轴交反比例函数y=﹣
(>0)的图象上任意一点,AB∥x轴交反比例函数y=﹣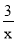 的图象于点B,以AB为边作平行四边形ABCD,其中C,D在x轴上,则平行四边形ABCD的面积为( )
的图象于点B,以AB为边作平行四边形ABCD,其中C,D在x轴上,则平行四边形ABCD的面积为( )
A. 2 B. 3 C. 4 D. 5
D 【解析】试题解析:因为四边形ABCD为平行四边形,它与同底等高的矩形面积相等,根据反比例函数中 的几何意义,易得矩形的面积为 ,所以平行四边形ABCD的面积为5. 故本题应选D.查看答案和解析>>
科目:初中数学 来源:黄金30题系列 九年级数学 小题好拿分 题型:单选题
如图,△DEF是由△ABC经过位似变换得到的,点O是位似中心,D,E,F分别是OA, OB,OC的中点,则△DEF与△ABC的面积比是( )
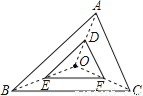
A. 1:2 B. 1:4 C. 1:5 D. 1:6
B 【解析】试题分析:由D,F分别是OA,OC的中点,根据三角形的中位线的性质得DF=AC,根据三角形相似的性质可知△DEF与△ABC的相似比是1:2,因此△DEF与△ABC的面积比是1:4. 故选B.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com