
如图,△DEF是由△ABC经过位似变换得到的,点O是位似中心,D,E,F分别是OA, OB,OC的中点,则△DEF与△ABC的面积比是( )
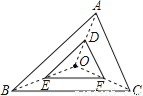
A. 1:2 B. 1:4 C. 1:5 D. 1:6
B 【解析】试题分析:由D,F分别是OA,OC的中点,根据三角形的中位线的性质得DF=AC,根据三角形相似的性质可知△DEF与△ABC的相似比是1:2,因此△DEF与△ABC的面积比是1:4. 故选B. 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:初中数学 来源:2018年春人教版八年级数学下册(广西)期中测试 题型:解答题
已知x,y是实数,且y=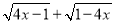 +3,求3
+3,求3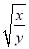 的值.
的值.
查看答案和解析>>
科目:初中数学 来源:2018年春人教版八年级数学下册(广西)期中测试 题型:单选题
如图,四边形ABCD中,AD∥BC,DE∥AB,DE=DC,∠C=80°,则∠A等于( )
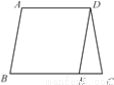
A. 80° B. 90° C. 100° D. 110°
C 【解析】∵DE=DC,∠C=80°, ∴∠DEC=80°, ∵AB∥DE, ∴∠B=∠DEC=80°, ∵AD∥BC, ∴∠A=180°-80°=100°, 故选C.查看答案和解析>>
科目:初中数学 来源:黄金30题系列 九年级数学 小题好拿分 题型:单选题
过⊙O内一点M的最长弦长为10cm,最短弦长为8cm,那么OM长为( )
A. 3cm B. 6cm C. 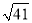 cm D. 9cm
cm D. 9cm
查看答案和解析>>
科目:初中数学 来源:青海省2017-2018学年七年级上学期12月月考数学试卷 题型:解答题
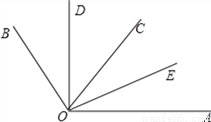
如图,OD平分∠BOC,OE平分∠AOC.若∠BOC=70°,∠AOC=50°.
(1)求出∠AOB及其补角的度数;
(2)请求出∠DOC和∠AOE的度数,并判断∠DOE与∠AOB是否互补,并说明理由.
查看答案和解析>>
科目:初中数学 来源:甘肃省定西市安定区2017-2018学年九年级上学期期末考试数学试卷 题型:解答题
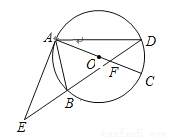
如图,⊙O的直径AC与弦BD相交于点F,点E是DB延长线上一点,∠EAB=∠ADB.
(1)求证:EA是⊙O的切线;
(2)已知点B是EF的中点,AF=4,CF=2,求AE的长.
查看答案和解析>>
科目:初中数学 来源:江苏省东台市第三教育联盟2017-2018学年度第一学期第三次阶段检测七年级数学试卷 题型:填空题
长方体的主视图与俯视图如图所示,则这个长方体的体积是________.
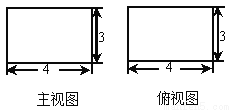
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com