
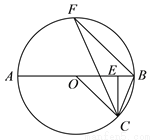
已知:如图, AB为⊙O的直径,CE⊥AB于E,BF∥OC,连接BC,CF.
求证:∠OCF=∠ECB.
科目:初中数学 来源:河南省商丘市2017-2018学年上期九年级数学期末第一次模拟试卷 题型:填空题
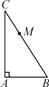
如图,点M是Rt△ABC的斜边BC上异于B,C的一点,过M点作直线截△ABC,使截得的三角形与△ABC相似,这样的直线共有________条.
查看答案和解析>>
科目:初中数学 来源:广东省江门市江海区五校2018届九年级上学期期末联考数学试卷 题型:单选题
下列事件中是必然事件的是( )
A. 打开电视,它正在播广告 B. 掷两枚质地均匀的骰子,点数之和一定大于6
C. 某射击运动员射击一次,命中靶心 D. 早晨的太阳从东方升起
D 【解析】A. 打开电视,它正在播广告是随机事件; B. 掷两枚质地均匀的骰子,点数之和一定大于6是不可能事件; C. 某射击运动员射击一次,命中靶心是随机事件; D. 早晨的太阳从东方升起是必然事件; 故选D.查看答案和解析>>
科目:初中数学 来源:山东省淄博市2017-2018学年七年级上学期期中考试数学试卷 题型:单选题
若│a∣= —a ,则a是( ).
A. 非负数 B. 非正数 C. 正数 D. 负数
B 【解析】 本题考查绝对值的性质。绝对值是非负的,故—a ≥0即a≤0,a为非正数。查看答案和解析>>
科目:初中数学 来源:山东省淄博市2017-2018学年七年级上学期期中考试数学试卷 题型:单选题
下列各图经过折叠后不能围成一个正方体的是( ).
A. 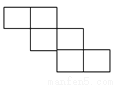 B.
B. 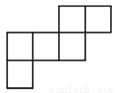 C.
C.  D.
D. 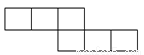
查看答案和解析>>
科目:初中数学 来源:北京市顺义区2018届初三上学期期末考试数学试卷 题型:解答题
如图,E是□ABCD的边BC延长线上一点,AE交CD于点F,FG∥AD交AB于点G.
(1)填空:图中与△CEF相似的三角形有__________;(写出图中与△CEF相似的所有三角形)
(2)从(1)中选出一个三角形,并证明它与△CEF相似.
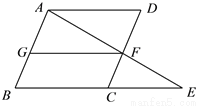
查看答案和解析>>
科目:初中数学 来源:北京市顺义区2018届初三上学期期末考试数学试卷 题型:填空题
如图标记了 △ABC与△DEF边、角的一些数据,如果再添加一个条件使△ABC∽△DEF,那么这个条件可以是__________.(只填一个即可)

查看答案和解析>>
科目:初中数学 来源:2017-2018学年陕西安市九年级(上)期末数学试卷 题型:解答题
某太阳能热水器的横截面示意图如图所示,已知真空热水管AB与支架CD所在直线相交于点O,且OB=OD,支架CD与水平线AE垂直,∠BAC=∠CDE=30°,DE=80cm,AC=165cm.
(1)求支架CD的长;
(2)求真空热水管AB的长.(结果保留根号)
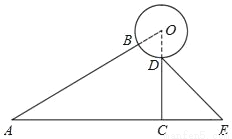
查看答案和解析>>
科目:初中数学 来源:北京市2017-2018学年第一学期八年级数学期中试卷 题型:填空题
若分式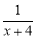 在实数范围内有意义,则
在实数范围内有意义,则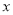 的取值范围是 .
的取值范围是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com