
下列每组数分别表示三根木棒的长,将它们首尾连接后,能摆成三角形的一组是( )
A. 1,2,1 B. 1,2,3 C. 1,2,2 D. 1,2,4
C 【解析】试题解析:三角形的三边关系为:任意两边之和大于第三边. A. 不能构成三角形. B. 不能构成三角形. C. 能构成三角形. D. 不能构成三角形. 故选C. 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:四川省自贡市2016-2017学年上学期八年级期末统一考试数学试卷 题型:解答题
仔细阅读材料,再尝试解决问题:
完全平方式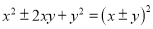 以及
以及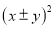 的值为非负数的特点在数学学习中有广泛的应用,比如探求
的值为非负数的特点在数学学习中有广泛的应用,比如探求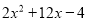 的最大(小)值时,我们可以这样处理:
的最大(小)值时,我们可以这样处理:
【解析】
原式 = 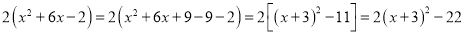 .
.
因为无论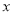 取什么数,都有
取什么数,都有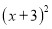 的值为非负数,所以
的值为非负数,所以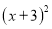 的最小值为0;此时
的最小值为0;此时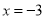 时,进而
时,进而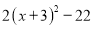 的最小值是
的最小值是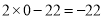 ;所以当
;所以当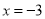 时,原多项式的最小值是
时,原多项式的最小值是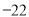 .
.
请根据上面的解题思路,探求:
⑴.多项式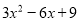 的最小值是多少,并写出对应的
的最小值是多少,并写出对应的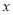 的取值;
的取值;
⑵.多项式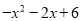 的最大值是多少,并写出对应的
的最大值是多少,并写出对应的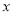 的取值.
的取值.
查看答案和解析>>
科目:初中数学 来源:2016-2017学年内蒙古呼和浩特市九年级(下)期中数学试卷 题型:单选题
下列运算正确的是( )
A. a2+a3=a5 B. (﹣2a2)3÷(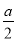 )2=﹣16a4
)2=﹣16a4
C. 3a﹣1=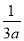 D. (2
D. (2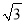 a2﹣
a2﹣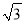 a)2÷3a2=4a2﹣4a+1
a)2÷3a2=4a2﹣4a+1
查看答案和解析>>
科目:初中数学 来源:浙江省宁波市东钱湖九校2017-2018学年八年级上册数学期中联考试卷 题型:填空题
若点M(1-m,2+m)在第四象限内,则m的取值范围是_______.
m<-2 【解析】试题解析:点在第四象限内, 解得: 故答案为:查看答案和解析>>
科目:初中数学 来源:浙江省宁波市东钱湖九校2017-2018学年八年级上册数学期中联考试卷 题型:单选题
已知点A(﹣3,2)与点B(x,y)在同一条平行x轴的直线上,且B点到y轴的距离等于2,则B点的坐标是( )
A. (﹣2,2) B. (2,﹣2) C. (﹣2,2)或(﹣2,﹣2) D. (﹣2,2)或(2, 2)
D 【解析】试题解析:∵点A(?3,2)与点在同一条平行轴的直线上, ∴ ∵B点到轴的矩离等于2, ∴即或 ∴B点的坐标为(?2,2)或(2,2). 故选D.查看答案和解析>>
科目:初中数学 来源:2017-2018学年江苏苏州姑苏区第十中学初二上期中试卷数学试卷 题型:解答题
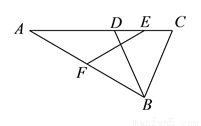
如图,在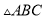 中,点
中,点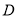 在边
在边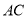 上,
上, 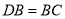 ,
, 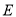 是
是 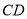 的中点,
的中点, 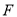 是
是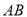 的中点,求证:
的中点,求证: 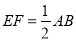 .
.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年江苏苏州姑苏区第十中学初二上期中试卷数学试卷 题型:填空题
如图,已知点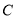 是线段
是线段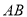 的中点,点
的中点,点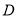 是线段
是线段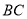 上的定点(不同于端点
上的定点(不同于端点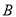 、
、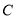 ),过点
),过点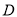 作直线
作直线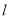 垂直线段
垂直线段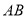 ,若点
,若点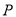 是直线
是直线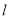 上任意一点,连接
上任意一点,连接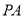 、
、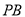 ,则能使
,则能使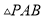 成为等腰三角形的点
成为等腰三角形的点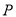 一共有__________个.(填写确切的数字)
一共有__________个.(填写确切的数字)
查看答案和解析>>
科目:初中数学 来源:江苏省2018届九年级上学期期末模拟数学试卷 题型:解答题
已知在平面直角坐标系xOy中,O为坐标原点,线段AB的两个端点A(0,2),B(1,0)分别在y轴和x轴的正半轴上,点C为线段AB的中点,现将线段BA绕点B按顺时针方向旋转90°得到线段BD,抛物线y=ax2+bx+c(a≠0)经过点D.
(1)如图1,若该抛物线经过原点O,且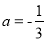 .
.
①求点D的坐标及该抛物线的解析式;
②连结CD,问:在抛物线上是否存在点P,使得∠POB与∠BCD互余?若存在,请求出所有满足条件的点P的坐标,若不存在,请说明理由;
(2)如图2,若该抛物线y=ax2+bx+c(a≠0)经过点E(1,1),点Q在抛物线上,且满足∠QOB与∠BCD互余.若符合条件的Q点的个数是3个,请直接写出a的值.
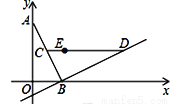
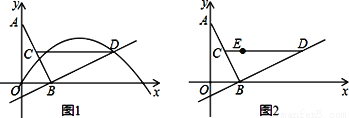
备用图
(1)①D的坐标是(3,1),y=﹣x2+x;②点P(, )或(,﹣);(2)a的值为a=. 【解析】试题分析: (1)①过点D作DF⊥x轴于点F,先通过三角形全等求得D的坐标,把D的坐标和a=﹣,c=0代入y=ax2+bx+c即可求得抛物线的解析式;②先证得CD∥x轴,进而求得要使得∠POB与∠BCD互余,则必须∠POB=∠BAO,设P的坐标为(x,﹣x2+x),分两种情况讨论即可求得;(...查看答案和解析>>
科目:初中数学 来源:山东省临朐县沂山风景区2017-2018学年七年级上期末模拟数学试卷 题型:填空题
数轴上的A点与表示﹣3的点距离4个单位长度,则A点表示的数为________.
﹣7或1 【解析】由于所求点在-3的哪侧不能确定,所以应分在-3的左侧和在-3的右侧两种情况讨论. 【解析】 当所求点在-3的左侧时,则距离4个单位长度的点表示的数是-3-4=-7; 当所求点在-3的右侧时,则距离4个单位长度的点表示的数是-3+4=1. 故答案为:-7或1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com