练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    解方程：x2﹣3x+1=0．

    x1=，x2=． 【解析】试题分析：运用一元二次方程的求根公式求解即可. 试题解析：∵a=1，b=-3，c=1 b2-4ac=（-3）2-4×1×1=5 ∴ 即： ，
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：北京市2018届九年级（上）期中数学试卷 题型：单选题

    如图，在纸上剪下一个圆形和一个扇形的纸片，使之恰好能围成一个圆锥模型．若圆的半径为r，扇形的半径为R，扇形的圆心角等于90°，则r与R之间的关系是( )

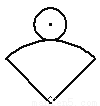
    A. R＝2r； B. 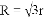； C. R＝3r； D. R＝4r．

    D 【解析】试题分析：利用圆锥的底面周长等于侧面展开图的扇形弧长，根据弧长公式计算．扇形的弧长是：，圆的半径为r，则底面圆的周长是2πr，圆锥的底面周长等于侧面展开图的扇形弧长则得到：=2πr，∴=2r，即：R=4r，r与R之间的关系是R=4r． 故选：D．

    查看答案和解析>>

    科目：初中数学 来源：河南省郑州市郑东新区实验学校2017-2018学年八年级（上）期中数学试卷 题型：解答题

    计算： ．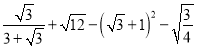

    . 【解析】试题分析：先根据二次根式的性质和利用完全平方公式计算，然后化简后合并即可． 试题解析： 原式=+2﹣（3+2+1）﹣ =+2﹣4﹣2﹣ =﹣．

    查看答案和解析>>

    科目：初中数学 来源：人教版八年级上册 第十三章 轴对称 13.1 轴对称 同步练习题 题型：解答题

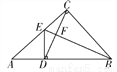
    如图所示,在△ABC中,∠ACB=90°,D是AB上一点,且BD=BC,过D作AB的垂线交AC于点E,连接CD,BE交于点F.求证:BE是CD的垂直平分线.

    证明见解析 【解析】试题分析：首先根据HL证明Rt△ECB≌Rt△EDB，得出∠EBC=∠EBD，然后根据等腰三角形底边上的高与顶角的平分线重合即可证明． 试题解析： 证明:∵DE⊥AB, ∴∠BDE=90°. ∵∠ACB=90°, ∴∠BDE=∠ACB=90°. 在Rt△BCE和Rt△BDE中, ∴Rt△BCE≌Rt△BDE(HL). ∴CE...

    查看答案和解析>>

    科目：初中数学 来源：人教版八年级上册 第十三章 轴对称 13.1 轴对称 同步练习题 题型：单选题

    如图所示,该图形的对称轴条数为( )

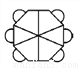
    A. 2 B. 4 C. 6 D. 8

    A 【解析】根据图示可以画出2条， 故选A．

    查看答案和解析>>

    科目：初中数学 来源：湖北省武汉市江夏区2018届九年级上期末模拟数学试卷 题型：单选题

    某厂前年缴税30万元，今年缴税36.3万元，若该厂缴税的年平均增长率为x，则可列方程（  ）

    A. 30x2=36.3 B. 30（1-x）2=36.3

    C. 30+30（1+x）+30（1+x）2=36.3 D. 30（1+x）2=36.3

    D 【解析】如果设该厂缴税的年平均增长率为x， 那么根据题意得今年缴税30（1+x)2 ， 列出方程为：30（1+x)2=36.3， 故选D．

    查看答案和解析>>

    科目：初中数学 来源：湖北省武汉市江夏区2018届九年级上期末模拟数学试卷 题型：单选题

    如图，点P在以AB为直径的半圆内，连接AP、BP，并延长分别交半圆于点C、D，连接AD、BC并延长交于点F，作直线PF，下列说法一定正确的是（   ）

    ①AC垂直平分BF；②AC平分∠BAF；③FP⊥AB；④BD⊥AF．

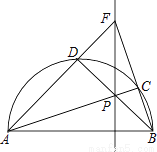
    A. ①③ B. ①④ C. ②④ D. ③④

    D 【解析】试题分析：①∵AB为直径，∴∠ACB=90°，∴AC垂直BF，但不能得出AC平分BF，故①错误，②如图1，连结CD， ∵AB为直径，∴∠ADB=90°，∴∠BDF=90°，假设AC平分∠BAF成立，则有DC=BC，∴在RT△FDB中，DC=BC=FC，∴AC⊥BF，且平分BF，∴AC垂直BF，但不能得出AC平分BF，与①中的AC垂直BF，但不能得出AC平分BF相矛盾，故②错...

    查看答案和解析>>

    科目：初中数学 来源：数学人教版八年级上册第11章第二节与三角形有关的角第三课时同步练习 题型：填空题

    将一副直角三角板如图放置，使含30°角的三角板的一段直角边与含45°角的三角板的一段直角边重合，则∠α的度数为 ．

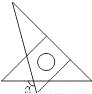
    105°． 【解析】试题解析：如图， ∠1=90°-30°=60°， 由三角形的外角性质得，∠α=∠1+45°=60°+45°=105°．

    查看答案和解析>>

    科目：初中数学 来源：浙江省宁波市东钱湖九校2018届九年级上册期中联考数学试卷 题型：解答题

    甲、乙两人进行羽毛球比赛，羽毛球飞行的路线为抛物线的一部分，如图，甲在O点正上方1m的P处发出一球，羽毛球飞行的高度y（m）与水平距离x（m）之间满足函数表达式y=a（x﹣4）2+h，已知点O与球网的水平距离为5m，球网的高度为1.55m．

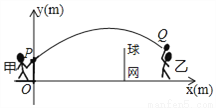
    （1）当a=﹣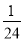时，①求h的值；②通过计算判断此球能否过网．

    （2）若甲发球过网后，羽毛球飞行到与点O的水平距离为7m，离地面的高度为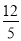m的Q处时，乙扣球成功，求a的值．

    （1）①，②能；（2）－ 【解析】试题分析：（1）①将点P（0，1）代入即可求得h；②求出x=5时，y的值，与1.55比较即可得出判断； （2）将（0，1）、（7， ）代入代入即可求得a、h． （1）①当a=时， ，将点P（0，1）代入，得： ×16+h=1，解得：h=； ②把x=5代入，得： =1.625，∵1.625＞1.55，∴此球能过网； （2）把（0，1）、...

    查看答案和解析>>

    同步练习册答案