
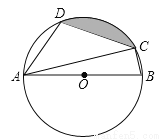
��ͼ���ı���ABCD�ǡ�O���ڽ��ı��Σ�AB�ǡ�O��ֱ������D=108�㣬����AC����1�����BAC�Ķ�������2������DAC=45�㣬DC=8����ͼ����Ӱ���ֵ�����������У���

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2017-2018ѧ�����꼶��ѧ�²ᣨ���壩�����м���� ���ͣ������
��ƽ��ֱ������ϵ�У���ABC���������������ֱ���A(��2��3)��B(��4����1)��C(2��0)������ABCƽ������A1B1C1��λ�ã���A��B��C�Ķ�Ӧ��ֱ��ǵ�A1��B1��C1������A1������Ϊ(3��1)�����C1������Ϊ___________��
(7����2) �������������������A��-2��3��ƽ�ƺ��A1������Ϊ��3��1�����ɵ�A��������5���������2�� ���C������仯��A��ı仯��ͬ����C1��2+5��0-2��������7��-2���� �ʴ�Ϊ����7��-2�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ɽ��ʡΫ���и�����2017-2018ѧ�����꼶���ϣ�������ѧ�Ծ� ���ͣ������
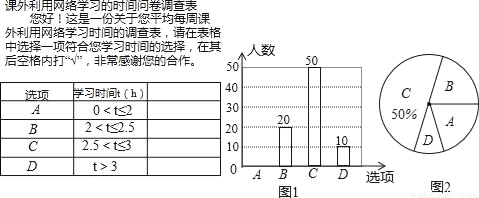
���Ž�����Ϣ���ķ�չ��ѧ����ѧϰ��ʽ�������࣬��ʦΪ��ָ��ѧ����Ч�����������ѧϰ����ѧ������������ʾ����飨�ʾ��������ͼ��ʾ�������õ�����������ͼ1��ͼ2����ͳ��ͼ�������������������ͳ��ͼ����������⣺
��1�����ν����ʾ������ѧ�������� ���ˣ�������ͳ��ͼ�С�D��ѡ����ռ�İٷֱ�Ϊ�� ����
��2������ͳ��ͼ�У���B��ѡ������Ӧ����Բ�Ľ�Ϊ�� ���ȣ�
��3���벹ȫ����ͳ��ͼ��
��4������У����1200��ѧ�����������Ƹ�Уѧ��������������ѧϰ��ʱ���ڡ�A��ѡ����ж����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ɽ��ʡΫ���и�����2017-2018ѧ�����꼶���ϣ�������ѧ�Ծ� ���ͣ���ѡ��
���й��ڡ���55������������ȷ���ǣ�������
A. �����ǩ�5 B. ָ����5 C. ��������� D. �루��5��5�����ͬ
B �����������ó˷��������жϿɵã� ����55����ָ����5. ��ѡ��B.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ɽ��ʡΫ���и�����2017-2018ѧ�����꼶���ϣ�������ѧ�Ծ� ���ͣ���ѡ��
����ͼ���У���������ͼ�ε��ǣ�������
A.  B.
B.  C.
C.  D.
D. 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㽭ʡ��Ҧ��2018����꼶��ѧ�����п�����ѧ�Ծ� ���ͣ������
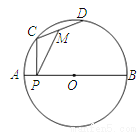
��ͼ��C��D����ABΪֱ����ԲO�ϵ��������㣨��C��D����A��B�غϣ������˶���������CDʼ�ձ��ֲ��䣬M����CD���е㣬����C��CP��AB�ڵ�P����CD=3��AB=5��PM=x����x�����ֵ��____
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㽭ʡ��Ҧ��2018����꼶��ѧ�����п�����ѧ�Ծ� ���ͣ���ѡ��
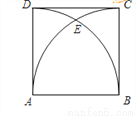
��ͼ,������ABCD�ı߳�AB=4,�ֱ��Ե�A��BΪԲ��,AB��Ϊ�뾶����,�������ڵ�E,��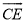 �ij���( )
�ij���( )
A. 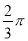 B.
B. 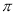 C.
C. 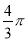 D.
D. 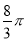
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ2017-2018ѧ�����꼶��ѧ�����п�����ѧ�Ծ� ���ͣ���ѡ��
��|a|��5��b����3����a��b��ֵΪ��������
A. 2��8 B. ��2��8 C. 2��8 D. ��2��8
B ����������|a|��5����a=5��5�� ��b����3�� ��a��b=8��2. ��ѡB.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��������2017-2018ѧ���һѧ�ڰ��꼶��ѧ�����Ծ� ���ͣ������
��ͼ�� ��
��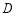 ��
�� ��
��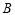 ��
�� ��
�� .��֤��
.��֤��
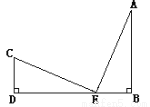
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com