
已知抛物线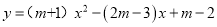 的图象与
的图象与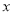 轴有两个公共点.
轴有两个公共点.
(1)求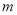 的取值范围,写出当
的取值范围,写出当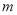 取其范围内最大整数时抛物线的解析式;
取其范围内最大整数时抛物线的解析式;
(2)将(1)中所求得的抛物线记为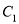 ,
,
①求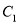 的顶点
的顶点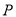 的坐标;
的坐标;
②若当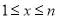 时,
时, 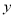 的取值范围是
的取值范围是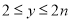 ,求
,求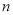 的值;
的值;
(3)将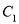 平移得到抛物线
平移得到抛物线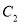 ,使
,使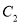 的顶点
的顶点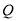 落在以原点为圆心半径为
落在以原点为圆心半径为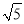 的圆上,求点
的圆上,求点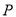 与
与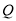 两点间的距离最大时
两点间的距离最大时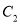 的解析式,怎样平移
的解析式,怎样平移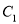 可以得到所求抛物线?
可以得到所求抛物线?

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源:江苏省苏州市区2017-2018学年第一学期九年级数学期末考试试卷 题型:解答题
分解因式:2x2+4x+2
2(x+1)2 【解析】试题分析:提取公因式法和公式法相结合. 试题解析:原式 故答案为:查看答案和解析>>
科目:初中数学 来源:辽宁省鞍山市铁西区2017-2018学年七年级(上)期中数学试卷 题型:单选题
某县12月份某一天的天气预报为气温﹣2~5℃,该天的温差为( )
A. ﹣3℃ B. ﹣7℃ C. 3℃ D. 7℃
D 【解析】∵5-(-2)=7℃, ∴该天的温差为7℃. 故选D.查看答案和解析>>
科目:初中数学 来源:福建省泉州台商投资区2017-2018学年八年级上学期期末教学质量检测数学试卷 题型:填空题
实数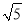 ,
, 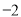 ,
, 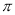 ,
, 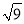 ,
, 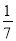 中,其中无理数出现的频数是______________.
中,其中无理数出现的频数是______________.
查看答案和解析>>
科目:初中数学 来源:福建省泉州台商投资区2017-2018学年八年级上学期期末教学质量检测数学试卷 题型:单选题
下列命题是假命题的是( )
A. 直角都相等 B. 对顶角相等 C. 同位角相等 D. 两点之间,线段最短
C 【解析】根据真假命题的概念,可知直角都相等是真命题,对顶角相等是真命题,两点之间,线段最短,是真命题,同位角相等的前提是两直线平行,故是假命题. 故选:C.查看答案和解析>>
科目:初中数学 来源:广东省广州市番禺区2018届九年级上学期期末考试数学试卷 题型:解答题
如图,在正方形网格中, 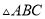 的三个顶点都在格点上,点
的三个顶点都在格点上,点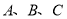 的坐标分别为
的坐标分别为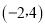 、
、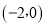 、
、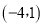 ,试解答下列问题:
,试解答下列问题:
(1)画出 关于原点
关于原点 对称的
对称的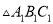 ;
;
(2)平移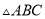 ,使点
,使点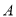 移到点
移到点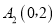 ,画出平移后的
,画出平移后的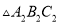 并写出点
并写出点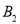 、
、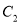 的坐标;
的坐标;
(3)在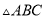 、
、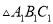 、
、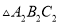 中,
中, 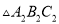 与哪个图形成中心对称?试写出其对称中心的坐标.
与哪个图形成中心对称?试写出其对称中心的坐标.

查看答案和解析>>
科目:初中数学 来源:广东省广州市番禺区2018届九年级上学期期末考试数学试卷 题型:填空题
抛物线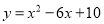 的对称轴为____.
的对称轴为____.
查看答案和解析>>
科目:初中数学 来源:海南省2017-2018学年度第一学期七年级数学期中试卷 题型:解答题
甲、乙两人要加工200个零件,甲先单独加工5小时,后与乙一起加工4小时完成了任务.已知甲每小时比乙多加工2个零件,分别求甲、乙两人每小时加工的零件个数.
甲每小时加工零件16个,乙每小时加工零件14个. 【解析】试题分析:如果乙每小时加工x个零件,那么甲每小时加工(x+2)个零件,根据要加工200个零件,甲先单独加工5小时,然后又与乙一起加工4小时,完成了任务以及甲每小时比乙多加工2个,可列出方程求解即可. 解:设乙每小时加工零件x个,则甲每小时加工零件(x+2)个. 根据题意,得5(x+2)+4(x+2+x)=200. 解...查看答案和解析>>
科目:初中数学 来源:甘肃省武威市2017-2018学年八年级(上)期中数学模拟试卷 题型:单选题
计算3ab2•5a2b的结果是( )
A. 8a2b2 B. 8a3b3 C. 15a3b3 D. 15a2b2
C 【解析】3ab2•5a2b=3×5a•a2•b2b=15a3b3, 故选C.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com