
��֪�� 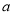 �����ĸ�������
�����ĸ������� 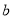 ����С������������
����С������������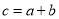 ����ش��������⣺
����ش��������⣺
��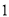 ����ֱ��д��
����ֱ��д��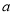 ��
�� 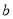 ��
�� 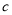 ��ֵ��
��ֵ�� 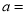 __________��
__________�� 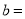 __________��
__________�� 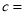 __________��
__________��
��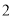 ��
��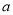 ��
�� 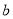 ��
�� 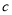 ������������Ӧ�ĵ�ֱ�Ϊ
������������Ӧ�ĵ�ֱ�Ϊ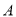 ��
�� 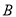 ��
�� 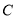 �����������ϱ�ʾ
�����������ϱ�ʾ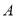 ��
�� 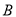 ��
�� 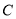 ���㣮
���㣮
��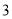 ���ڣ�
���ڣ�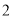 ��������£���
��������£��� ��
��  ��
�� 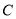 ��ʼ���������˶�������
��ʼ���������˶�������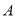 ����
����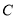 ����ÿ��
����ÿ��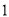 ����λ���ٶ������˶���ͬʱ����
����λ���ٶ������˶���ͬʱ����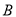 ��ÿ��
��ÿ��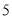 ����λ���ȵ��ٶ������˶�������
����λ���ȵ��ٶ������˶�������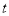 ���������
���������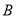 ���
���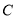 ֮��ľ����ʾΪ
֮��ľ����ʾΪ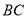 ����
����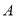 ���
���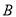 ֮��ľ����ʾΪ
֮��ľ����ʾΪ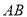 ������
������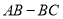 ��ֵ�Ƿ�����ʱ��
��ֵ�Ƿ�����ʱ��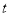 �ı仯���仯�����仯����˵�����ɣ������䣬�����
�ı仯���仯�����仯����˵�����ɣ������䣬�����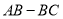 ��ֵ��
��ֵ��

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ���㽭������ɽ��������ѧ2017-2018ѧ�����꼶��ѧ��������ѧ�Ծ� ���ͣ������
�Ƚϴ�С��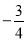
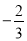 .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��������2017-2018ѧ�����꼶��ѧ�����п�����ѧ�Ծ� ���ͣ������
��֪��ͼ���������ϵ�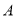 ��
�� 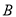 ����Ӧ������
����Ӧ������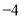 ��
�� 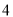 ��
��
���ڹ���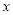 �Ĵ���ʽ
�Ĵ���ʽ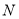 �����ǹ涨����������
�����ǹ涨����������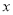 ������������Ӧ�ĵ�Ϊ
������������Ӧ�ĵ�Ϊ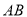 ֮�䣨������
֮�䣨������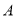 ��
�� 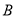 ��������һ��ʱ������ʽ
��������һ��ʱ������ʽ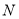 ȡ������ֵ�����ֵС�ڵ���
ȡ������ֵ�����ֵС�ڵ���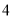 ����Сֵ���ڵ���
����Сֵ���ڵ���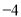 ����ƴ���ʽ
����ƴ���ʽ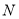 �����߶�
�����߶�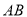 �ķ�մ���ʽ��
�ķ�մ���ʽ��
���磬���ڹ���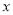 �Ĵ���ʽ
�Ĵ���ʽ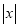 ����
����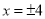 ʱ������ʽ
ʱ������ʽ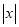 ȡ�����ֵ��
ȡ�����ֵ��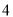 ����
����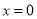 ʱ������ʽ
ʱ������ʽ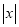 ȡ����Сֵ��
ȡ����Сֵ��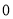 �����Դ���ʽ
�����Դ���ʽ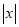 ���߶�
���߶�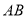 �ķ�մ���ʽ��
�ķ�մ���ʽ��
���⣺��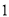 ������
������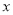 ����ʽ
����ʽ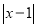 ����������
����������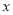 ������������Ӧ�ĵ�Ϊ
������������Ӧ�ĵ�Ϊ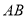 ֮�䣨������
֮�䣨������ ��
��  ��������һ��ʱ��ȡ�õ����ֵ����Сֵ�ֱ���__________��
��������һ��ʱ��ȡ�õ����ֵ����Сֵ�ֱ���__________��
���Դ���ʽ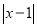 __________�����ǻ��ǣ��߶�
__________�����ǻ��ǣ��߶�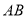 �ķ�մ���ʽ��
�ķ�մ���ʽ��
��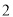 �����¹�
�����¹�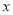 �Ĵ���ʽ��
�Ĵ���ʽ��
��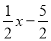 ����
����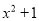 ����
����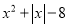 ����
����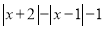 ��
��
���߶�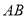 �ķ�մ���ʽ��__________����֤����ֻ��Ҫ֤�����߶�
�ķ�մ���ʽ��__________����֤����ֻ��Ҫ֤�����߶�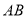 �ķ�մ���ʽ��ʽ�ӣ����ǵIJ���֤������
�ķ�մ���ʽ��ʽ�ӣ����ǵIJ���֤������
��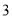 ������
������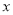 �Ĵ���ʽ
�Ĵ���ʽ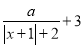 ���߶�
���߶�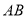 �ķ�մ���ʽ����������
�ķ�մ���ʽ����������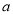 �����ֵ��__________����Сֵ��__________��
�����ֵ��__________����Сֵ��__________��
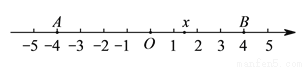
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��������2017-2018ѧ�����꼶��ѧ�����п�����ѧ�Ծ� ���ͣ������
����ʽ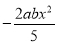 ��ϵ����__________��
��ϵ����__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��������2017-2018ѧ�����꼶��ѧ�����п�����ѧ�Ծ� ���ͣ���ѡ��

A. ������ŦԼ��ʱ��Ϊ13Сʱ
B. ����������ʱ��Ϊ13Сʱ
C. ������ŦԼ��ʱ��Ϊ14Сʱ
D. ����������ʱ��Ϊ14Сʱ
B ������������������������ع��ʱ�ʱ��IJ���Ϊʱ���������������������㣬��ȥһ�������ڼ�����������෴������˿�����ŦԼ��ʱ��Ϊ9������5��=14Сʱ������������ʱ��Ϊ9������4��=13Сʱ��������ŦԼ��ʱ��Ϊ8������5��=13Сʱ������������ʱ��Ϊ8������4��=12Сʱ�� ��ѡB���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㽭����������2016-2017ѧ�����꼶��ѧ����ĩ��ѧ�Ծ� ���ͣ������
�ⷽ��
��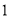 ��
��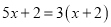
��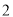 ��
��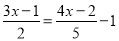
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㽭����������2016-2017ѧ�����꼶��ѧ����ĩ��ѧ�Ծ� ���ͣ������
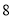 ��������Ϊ__________��
��������Ϊ__________�� 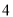 ��ƽ����Ϊ__________��
��ƽ����Ϊ__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㽭���ݹ�������������2017-2018ѧ�����꼶��ѧ��������ѧ ���ͣ������
�����ⷽ��
��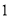 ��
�� �� ��
�� �� ��
��
��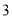 ��
�� �� ��
�� �� ��
�� ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2018�˽̰���꼶��ѧ�²���ϰ���ڶ�ʮ�´����� ���ͣ������
δ�������ֵ��ӱ�����ʱ����������ͳ��
| ƽ���� | ���� |
�� | 0.4 | 0.026 |
�� | 0.4 | 0.137 |
�������ֵ��ӱ���ʱ�ȶ������� ����
�� ������������������ķ�����0.026���ҵķ�����0.137�� 0.026��0.137�� �������ֵ��ӱ���ʱ�ȶ����Ǽף� �ʴ�Ϊ���ף��鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com