

A. 汉城与纽约的时差为13小时
B. 汉城与多伦多的时差为13小时
C. 北京与纽约的时差为14小时
D. 北京与多伦多的时差为14小时
B 【解析】试题分析:理解两地国际标准时间的差简称为时差.根据有理数减法法则计算,减去一个数等于加上这个数的相反数.因此可求汉城与纽约的时差为9﹣(﹣5)=14小时;汉城与多伦多的时差为9﹣(﹣4)=13小时;北京与纽约的时差为8﹣(﹣5)=13小时;北京与多伦多的时差为8﹣(﹣4)=12小时. 故选B.科目:初中数学 来源:浙江杭州萧山区高桥中学2017-2018学年七年级上学期期中数学试卷 题型:解答题
在数轴上表示数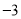 ,
, 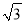 ,
, 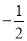 ,
, 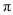 ,并把这组数从小到大用“
,并把这组数从小到大用“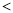 ”号连接起来.
”号连接起来.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年八年级数学人教版上册 第11章 三角形 单元测试卷 题型:单选题
在四边形ABCD中,∠A=∠B=∠C,点E在边AB上,∠AED=60°,则一定有( )
A. ∠ADE=20° B. ∠ADE=30° C. ∠ADE=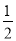 ∠ADC D. ∠ADE=
∠ADC D. ∠ADE=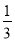 ∠ADC
∠ADC
查看答案和解析>>
科目:初中数学 来源:北京市2017-2018学年七年级上学期期中考试数学试卷 题型:填空题
小莎喜欢剪纸,某天看到了一扇漂亮的窗户(如图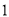 ),它是由一个大的正方形和一个半圆构成的.她就想到了利用长方形纸片(如图
),它是由一个大的正方形和一个半圆构成的.她就想到了利用长方形纸片(如图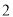 ,长方形的长是
,长方形的长是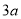 ,宽是
,宽是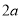 )来剪成类似的窗户纸片(如图
)来剪成类似的窗户纸片(如图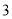 ,半圆的直径是
,半圆的直径是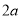 ).问原长方形纸片周长是__________,小莎剪去纸片(不要的部分)的面积是__________(用含
).问原长方形纸片周长是__________,小莎剪去纸片(不要的部分)的面积是__________(用含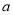 的代数式表示,保留
的代数式表示,保留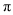 ).
).



查看答案和解析>>
科目:初中数学 来源:北京市2017-2018学年七年级上学期期中考试数学试卷 题型:单选题
如图,在一底面为长方形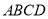 (长
(长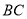 为
为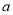 ,宽
,宽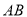 为
为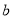 )的盒子底部,不重叠的放两张形状大小完全相同的两个长方形卡片,
)的盒子底部,不重叠的放两张形状大小完全相同的两个长方形卡片, 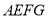 ,
, 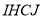 (长为
(长为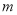 ,宽为
,宽为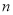 ),盒子底面未被卡片覆盖的部分用阴影表示,则图中两块阴影部分(长方形
),盒子底面未被卡片覆盖的部分用阴影表示,则图中两块阴影部分(长方形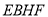 和
和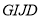 )的周长和是( ).
)的周长和是( ).

A. 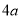 B.
B. 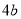 C.
C. 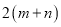 D.
D. 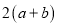
查看答案和解析>>
科目:初中数学 来源:浙江杭州西湖区2016-2017学年七年级上学期期末数学试卷 题型:解答题
已知: 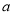 是最大的负整数,
是最大的负整数, 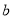 是最小的正整数,且
是最小的正整数,且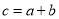 ,请回答下列问题:
,请回答下列问题:
(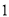 )请直接写出
)请直接写出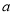 ,
, 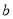 ,
, 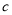 的值,
的值, 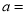 __________;
__________; 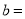 __________;
__________; 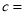 __________.
__________.
(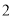 )
)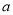 ,
, 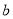 ,
, 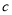 在数轴上所对应的点分别为
在数轴上所对应的点分别为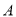 ,
, 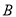 ,
, 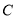 ,请在数轴上表示
,请在数轴上表示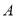 ,
, 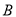 ,
, 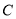 三点.
三点.
(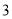 )在(
)在(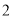 )的情况下,点
)的情况下,点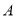 ,
, 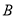 ,
, 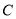 开始在数轴上运动,若点
开始在数轴上运动,若点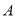 、点
、点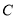 都以每秒
都以每秒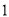 个单位的速度向左运动,同时,点
个单位的速度向左运动,同时,点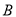 以每秒
以每秒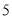 个单位长度的速度向右运动,假设
个单位长度的速度向右运动,假设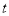 秒过后,若点
秒过后,若点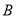 与点
与点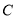 之间的距离表示为
之间的距离表示为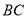 ,点
,点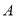 与点
与点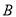 之间的距离表示为
之间的距离表示为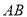 .请问
.请问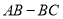 的值是否随着时间
的值是否随着时间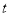 的变化而变化?若变化,请说明理由;若不变,请求出
的变化而变化?若变化,请说明理由;若不变,请求出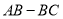 的值.
的值.
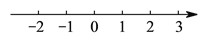
查看答案和解析>>
科目:初中数学 来源:浙江杭州西湖区2016-2017学年七年级上学期期末数学试卷 题型:填空题
如图是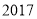 年
年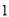 月份的日历表,现用一个矩形的日历表中任意框出
月份的日历表,现用一个矩形的日历表中任意框出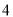 个数,则:
个数,则:
(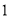 )
)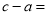 __________.
__________.
(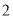 )当
)当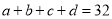 时,
时, 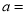 __________.
__________.
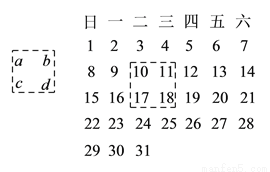
查看答案和解析>>
科目:初中数学 来源:浙江杭州拱墅区锦绣育才2017-2018学年七年级上学期期中数学 题型:解答题
温州和杭州某厂同时生产某种型号的机器若干台,温州厂可支援外地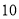 台,杭州厂可支援外地
台,杭州厂可支援外地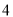 台.现在决定给武汉
台.现在决定给武汉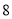 台,南昌
台,南昌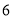 台.每台机器的运费(单位:百元)如表.设杭州运往南昌的机器为
台.每台机器的运费(单位:百元)如表.设杭州运往南昌的机器为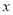 台.
台.
南昌 | 武汉 | |
温州厂 |
|
|
杭州厂 |
|
|
(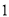 )用
)用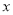 的代数式来表示总运费(单位:百元).
的代数式来表示总运费(单位:百元).
(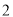 )若总运费为
)若总运费为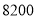 元,则杭州运往南昌的机器应为多少台?
元,则杭州运往南昌的机器应为多少台?
(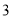 )试问有无可能使总运费是
)试问有无可能使总运费是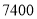 元?若有可能,请写出相应的调运方案;若无可能,请说明理由.
元?若有可能,请写出相应的调运方案;若无可能,请说明理由.
查看答案和解析>>
科目:初中数学 来源:2018人教版八年级数学下册练习:第二十章达标检测卷 题型:解答题
如图,是交警在一个路口统计的某个时段来往车辆的车速(单位:km/h).
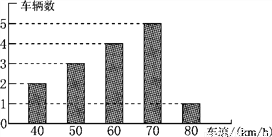
(1)计算这些车的平均速度.
(2)车速的众数是多少?
(3)车速的中位数是多少?
(1)60 km/h;(2)70 km/h;(3)60 km/h 【解析】试题分析:(1)根据频数分布直方图,利用加权平均数的定义可求得;(2)因为出现次数最多的数据是一组数据的众数,所以众数是70;(3)将一组数据按照从小到大的顺序排列,当有奇数个数据时,中位数是最中间的数据,当有偶数个数据时,中位数是最中间的两个数据的平均数. 试题解析:(1)这些车的平均速度是:(40×2+50×...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com