
先化简,再求值:
(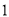 )
)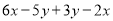 ,其中
,其中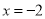 ,
, 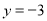 .
.
(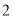 )
)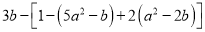 ,其中
,其中 ,
, 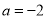 .
.
科目:初中数学 来源:福建省泉州台商投资区2017-2018学年七年级上学期期末教学质量检测数学试卷 题型:解答题
计算: 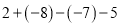
查看答案和解析>>
科目:初中数学 来源:浙江省宁波市鄞州区九校2017-2018学年八年级上学期期末考试数学试卷 题型:解答题
△ABC和△ADE都是等腰直角三角形, ∠BAC=∠DAE=90°.
(1)如图1,点D,E在AB,AC上,则BD,CE满足怎样的数量关系和位置关系?(直接写出答案)
(2)如图2,点D在△ABC内部, 点E在△ABC外部,连结BD, CE, 则BD,CE满足怎样的数量关系和位置关系?请说明理由.
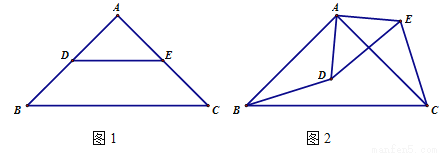
(3)如图3,点D,E都在△ABC外部,连结BD, CE, CD, EB,BD, 与CE相交于H点.
①若BD=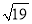 ,求四边形BCDE的面积;
,求四边形BCDE的面积;
②若AB=3,AD=2,设CD2=x,EB2=y,求y与x之间的函数关系式.

查看答案和解析>>
科目:初中数学 来源:浙江省宁波市鄞州区九校2017-2018学年八年级上学期期末考试数学试卷 题型:单选题
不等式-2x+6>0的正整数解有( )
A. 无数个 B. 0个 C. 1个 D. 2个
D 【解析】不等式的解集是x<3,故不等式?2x+6>0的正整数解为1,2. 故选:D.查看答案和解析>>
科目:初中数学 来源:浙江杭州下城区安吉路实验学校2017-2018学年七年级上学期期中数学试卷 题型:解答题
已知数轴上两点 、
、 对应的数分别为
对应的数分别为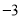 、
、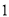 ,点
,点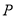 为数轴上一动点,其对应的数为
为数轴上一动点,其对应的数为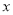 .
.
(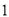 )若点
)若点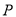 到点
到点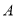 ,点
,点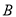 的距离相等,求点
的距离相等,求点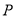 对应的数.
对应的数.
(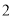 )数轴上是否存在点
)数轴上是否存在点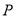 ,使点
,使点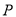 到点
到点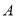 、点
、点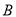 的距离之和为
的距离之和为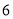 ?若存在,请求出
?若存在,请求出 的值;若不存在,说明理由.
的值;若不存在,说明理由.
(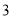 )点
)点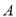 、点
、点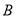 分别以
分别以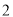 个单位长度/分、
个单位长度/分、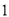 个单位长度/分的速度向右运动,同时点
个单位长度/分的速度向右运动,同时点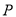 以
以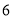 个单位长度/分的速度从
个单位长度/分的速度从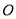 点向左运动.当遇到
点向左运动.当遇到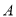 时,点
时,点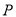 立即以同样的速度向右运动,并不停地往返于点
立即以同样的速度向右运动,并不停地往返于点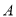 与点
与点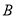 之间,求当点
之间,求当点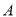 与点
与点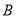 重合时,点
重合时,点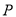 所经过的总路程是多少?
所经过的总路程是多少?
查看答案和解析>>
科目:初中数学 来源:浙江杭州下城区安吉路实验学校2017-2018学年七年级上学期期中数学试卷 题型:填空题
已知实数x,y满足|x﹣4|+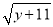 =0,则代数式x﹣y=__.
=0,则代数式x﹣y=__.
查看答案和解析>>
科目:初中数学 来源:浙江杭州下城区安吉路实验学校2017-2018学年七年级上学期期中数学试卷 题型:单选题
如果单项式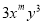 和
和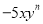 是同类项,则
是同类项,则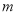 和
和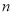 的值是( )
的值是( )
A. 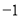 ,
, 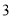 B.
B. 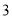 ,
, 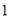 C.
C. 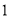 ,
, 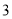 D.
D. 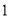 ,
, 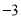
查看答案和解析>>
科目:初中数学 来源:福建省南平市2017-2018学年第一学期八年级期末质量检测数学试卷 题型:填空题
已知等腰三角形的一个底角为70°,则它的顶角为_______.
40° 【解析】∵等腰三角形的一个底角为70° ∴顶角=180°?70°×2=40°. 故答案为:40°查看答案和解析>>
科目:初中数学 来源:新疆阿克苏十二中2017-2018学年八年级(上)期中数学试卷 题型:解答题
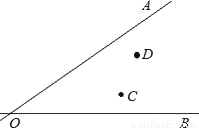
如图所示,107国道OA和320国道OB在某巿相交于O点,在∠AOB的内部有工厂C和D,现要建一个货站P,使P到OA和OB的距离相等,且使PC=PD,用尺规作出P点的位置.(不写作法,保留作图痕迹,写出结论)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com