
如果反比例函数y=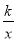 的图象经过点(3,
的图象经过点(3, 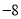 ),则该函数的解析式为( )
),则该函数的解析式为( )
A. y=-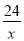 B. y=
B. y=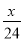 C. y=
C. y=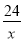 D. y=-
D. y=-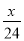
 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源:2017-2018学年九年级数学北师大版上册 第2章 一元二次方程 单元测试卷 题型:单选题
方程x2﹣2x+3=0的根的情况是( )
A. 有两个相等的实数根 B. 只有一个实数根
C. 没有实数根 D. 有两个不相等的实数根
C 【解析】试题分析:利用根的判别式进行判断. 【解析】 ∵ ∴此方程无实数根. 故选C.查看答案和解析>>
科目:初中数学 来源:北师大版九年级下册数学全册综合测试卷二 题型:填空题
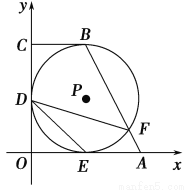
如图,在直角坐标系中,四边形OABC是直角梯形,BC∥OA,⊙P分别与OA、OC、BC相切于点E、D、B,与AB交于点F.已知A(2,0),B(1,2),则tan∠FDE=________.
查看答案和解析>>
科目:初中数学 来源:北师大版九年级下册数学全册综合测试卷二 题型:单选题
把二次函数y=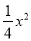 +x﹣1化为y=a(x﹣h)2+k的形式是( )
+x﹣1化为y=a(x﹣h)2+k的形式是( )
A. y=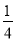 (x+1)2+2 B. y=
(x+1)2+2 B. y=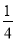 (x+1)2﹣2 C. y=
(x+1)2﹣2 C. y=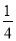 (x﹣2)2+2 D. y=
(x﹣2)2+2 D. y=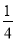 (x+2)2﹣2
(x+2)2﹣2
查看答案和解析>>
科目:初中数学 来源:2017-2018学年度人教版九年级数学下册第26 章同步课时练习:26.1.1 反比例函数 题型:填空题
反比例函数y=-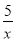 ,当x=-3时,y=___________.
,当x=-3时,y=___________.
查看答案和解析>>
科目:初中数学 来源:北师大版九年级下册数学全册综合测试卷一 题型:解答题
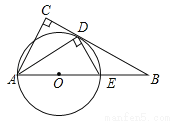
如图,在△ABC中,∠C=90°,∠BAC的平分线交BC于点D,DE⊥AD,交AB于点E,AE为⊙O的直径.
(1)判断BC与⊙O的位置关系,并证明你的结论;
(2)求证:△ABD∽△DBE;
(3)若cosB=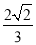 ,AE=4,求CD.
,AE=4,求CD.
查看答案和解析>>
科目:初中数学 来源:北师大版九年级下册数学全册综合测试卷一 题型:填空题
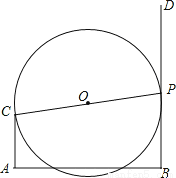
如图,CA⊥AB,DB⊥AB,已知AC=2,AB=6,点P射线BD上一动点,以CP为直径作⊙O,点P运动时,若⊙O与线段AB有公共点,则BP最大值为 .
查看答案和解析>>
科目:初中数学 来源:北师大版九年级下册数学全册综合测试卷一 题型:单选题
已知⊙O的半径为5,点P到圆心O的距离为6,那么点P与⊙O的位置关系是( )
A. 点P在⊙O上 B. 点P在⊙O内 C. 点P在⊙O外 D. 无法确定
C 【解析】试题解析:∵⊙O的半径为5,点P到圆心O的距离为6, ∴点P到圆心O的距离大于圆的半径, ∴点P在⊙O外. 故选C.查看答案和解析>>
科目:初中数学 来源:人教版七年级下册数学第7-10章综合测试卷 题型:填空题
方程组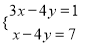 的解是 ________.
的解是 ________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com