
下列命题中,真命题是( )
A. 两条对角线相等的四边形是矩形
B. 两条对角线互相垂直的四边形是菱形
C. 两条对角线互相垂直且相等的四边形是正方形
D. 两条对角线互相平分的四边形是平行四边形
D 【解析】A.等腰梯形的对角线也相等,实际上可以任意旋转两条等长的相交线段,就能够得到无数对角线相等的四边形,但他们完全可以不是矩形,故A选项错误;B.如果一个四边形的对角线互相垂直,但是并没有互相平分的情形,只要让一条对角线平移,也可以得到无数不同的四边形,他们完全可以不是菱形,故B选项错误;C.只要适当选择角度,等腰梯形也可以满足题设条件,同样利用平移的技巧可以得到很多不同的四边形,故... 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:初中数学 来源:安徽省豪州市心校2017-2018学年度第一学期期末八年级数学试卷 题型:解答题
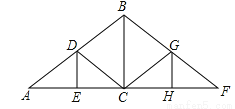
如图是屋架设计图的一部分,其中∠A=30°,点D是斜梁AB的中点,BC、DE垂直于横梁AC,AB=8cm,则立柱BC,DE要多长?
查看答案和解析>>
科目:初中数学 来源:四川省遂宁市蓬溪县2017-2018学年七年级上学期期末考试数学试卷 题型:单选题
如果a+b<0,并且ab>0,那么( ).
A. a>0,b>0 B. a<0,b<0 C. a<0,b>0 D. a>0,b<0
B 【解析】由ab>0可得:a、b同号; 由a+b<0可得:a<0,b<0. 故选B.查看答案和解析>>
科目:初中数学 来源:山东省济南市历城区2018届九年级上学期期末考试数学试卷 题型:填空题
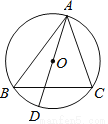
如图,⊙O是△ABC的外接圆,AD是⊙O的直径,若⊙O的半径为5,AC=8.则cosB的值是_________.
查看答案和解析>>
科目:初中数学 来源:山东省济南市历城区2018届九年级上学期期末考试数学试卷 题型:单选题
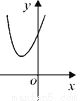
已知二次函数y = (x-m)2 +n的图象如图所示,则一次函数y = mx + n 与反比例函数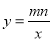 的图象可能是( )
的图象可能是( )
A. 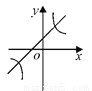 B.
B. 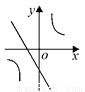 C.
C. 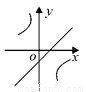 D.
D. 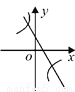
查看答案和解析>>
科目:初中数学 来源:河北省唐山市路北区2017-2018学年度第一学期学生素质终期评价七年级数学试卷 题型:解答题
已知线段AB=30cm
(1)如图1,点P沿线段AB自点A向点B以2cm/s的速度运动,同时点Q沿线段点B向点A以3cm/s的速度运动,几秒钟后,P、Q两点相遇?
(2)如图1,几秒后,点P、Q两点相距10cm?
(3)如图2,AO=4cm,PO=2cm,当点P在AB的上方,且∠POB=60°时,点P绕着点O以30度/秒的速度在圆周上逆时针旋转一周停止,同时点Q沿直线BA自B点向A点 运动,假若点P、Q两点能相遇,求点Q的运动速度.
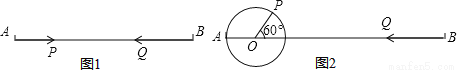
查看答案和解析>>
科目:初中数学 来源:河北省唐山市路北区2017-2018学年度第一学期学生素质终期评价七年级数学试卷 题型:解答题
18+42÷(-2)-(-3)2×5.
-35 【解析】18+42÷(-2)-(-3)2×5 =18+16÷(-2)-9×5 =18-8-45 =10-45 =-35查看答案和解析>>
科目:初中数学 来源:河北省唐山市路北区2017-2018学年度第一学期学生素质终期评价七年级数学试卷 题型:单选题
A. ﹣3 B. ﹣2 C. 0 D. 1
A 【解析】试题分析:|﹣3|>|﹣2|>>|0|, 故选A.查看答案和解析>>
科目:初中数学 来源:上海市虹口区2017学年九年级第一学期期终教学质量监控测试 题型:填空题
如果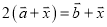 ,那么
,那么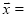 _______(用向量
_______(用向量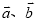 表示向量
表示向量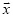 ).
).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com