
如果2是方程x2﹣3x+k=0的一个根,则常数k的值为( )
A. 1 B. 2 C. ﹣1 D. ﹣2
B 【解析】把x=2代入x2-3x+k=0,得 22-3×2+k=0, ∴k=2. 故选B. 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源:2017-2018学年七年级数学北师大版上册:第2章 有理数及其运算 单元测试卷 题型:解答题
画出数轴,在数轴上表示下列各数,并用“>”把它们连接起来.
-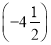 ,-2,0,(-1)2,|-3|,-3
,-2,0,(-1)2,|-3|,-3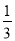 .
.
查看答案和解析>>
科目:初中数学 来源:四川省仁寿县2017-2018学年上学期八年级期末考试数学试卷 题型:单选题
若分式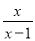 有意义,则x的取值范围是( )
有意义,则x的取值范围是( )
A. x≠-1; B. x≠1; C. x≥-1; D. x≥1.
B 【解析】∵分式有意义, ∴,解得: ,即的取值范围是: . 故选D.查看答案和解析>>
科目:初中数学 来源:北师大版七年级下册 第一章 整式的乘除 1.1 同底数幂的乘法 同步测试 含答案 题型:解答题
计算:
(-8)12×(-8)5.
-817 【解析】试题分析:按同底数幂的乘法进行计算即可. 试题解析:(-8)12×(-8)5=(-8)12+5=-817.查看答案和解析>>
科目:初中数学 来源:2018届中考数学一轮复习单元检测:第7讲 一元二次方程(组)及应用 题型:填空题
在△ABC中BC=2,AB=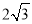 ,AC=b,且关于x的方程
,AC=b,且关于x的方程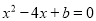 有两个相等的实数根,则AC边上的中线长为______.
有两个相等的实数根,则AC边上的中线长为______.
查看答案和解析>>
科目:初中数学 来源:2018届中考数学一轮复习单元检测:第7讲 一元二次方程(组)及应用 题型:解答题
解方程(1)6x2-5x+1=0; (2)(2x-1)2=x(3x+2)-7.
(1) x1=,x2=;(2) x1=2,x2=4 【解析】试题分析:本题考查了一元二次方程的解法,(1)用因式分解法中的十字相乘法分解因式求解;(2)先配方,再两边开平方. 【解析】 (1)(3x-1)(2x-1)=0. 则3x-1=0或2x-1=0,所以x1=,x2=. (2)4x2-4x+1=3x2+2x-7. x2-6x=-(x-3)2=1.x-3=±1, ...查看答案和解析>>
科目:初中数学 来源:浙江杭州上城区建兰中学2018届九年级上学期期中数试卷 题型:解答题
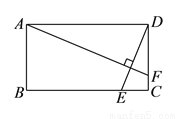
如图,矩形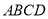 中,
中, 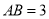 ,
, 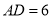 ,动点
,动点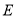 在边
在边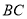 上,连结
上,连结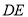 ,过点
,过点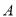 作
作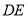 的垂线
的垂线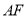 ,交直线
,交直线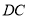 于点
于点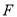 .设
.设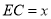 ,
, 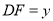 .
.
(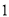 )求
)求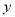 关于
关于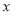 的函数关系式.
的函数关系式.
(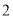 )当
)当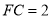 时,求
时,求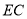 的长.
的长.
( )若直线
)若直线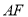 与线段
与线段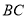 延长线交于点
延长线交于点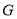 ,当
,当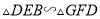 时,求
时,求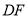 的长.
的长.
查看答案和解析>>
科目:初中数学 来源:浙江杭州上城区建兰中学2018届九年级上学期期中数试卷 题型:单选题
如图,在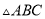 中,
中, 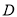 是线段
是线段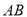 上的点,且
上的点,且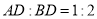 ,
, 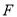 是线段
是线段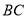 上的点,
上的点, 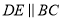 ,
, 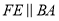 .小亮同学随机在
.小亮同学随机在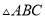 内部区域投针,则针扎到
内部区域投针,则针扎到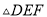 (阴影)区域内的概率是( )
(阴影)区域内的概率是( )
A. 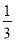 B.
B. 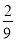 C.
C. 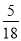 D.
D. 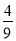
查看答案和解析>>
科目:初中数学 来源:人教版九年级下册数学全册综合测试一 题型:解答题
如图,抛物线y= 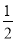 x2+bx﹣2与x轴交于A、B两点,与y轴交于C点,且A(﹣1,0).
x2+bx﹣2与x轴交于A、B两点,与y轴交于C点,且A(﹣1,0).
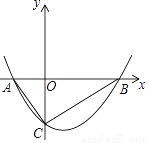
(1)求抛物线的解析式;
(2)判断△ABC的形状,证明你的结论.
(1)y= x2﹣ x﹣2;(2)见解析 【解析】试题分析:(1)因为点A在抛物线上,所以将点A代入函数解析式即可求得; (2)由函数解析式可以求得其与x轴、y轴的交点坐标,即可求得AB、BC、AC的长,由勾股定理的逆定理可得三角形的形状. 试题解析:(1)∵点A(-1,0)在抛物线y=x2+bx-2上, ∴×(-1)2+b×(-1)-2=0,b=- ∴抛物线的解析式...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com