
已知点A(﹣2m+4,3m﹣1)关于原点的对称点位于第四象限,则m的取值范围是 .
m>2. 【解析】 试题分析:直接利用关于原点对称点的性质得出关于m的不等式进而求出答案. 【解析】 ∵点A(﹣2m+4,3m﹣1)关于原点的对称点位于第四象限, ∴﹣(﹣2m+4)>0,﹣(3m﹣1)<0, 解得:m>2 则m的取值范围是:m>2. 故答案为:m>2.科目:初中数学 来源:黑龙江省大庆市(五四制)2017-2018学年七年级上学期期中考试数学试卷 题型:单选题
下列算式能用平方差公式计算的是( )
A. 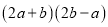 B.
B. 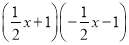
C.  D.
D. 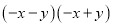
查看答案和解析>>
科目:初中数学 来源:陕西省2016-2017学年八年级下学期期末考试数学试卷 题型:单选题
下列分式是最简分式的是( ).
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源:数学人教版八年级上册第11章第二节与三角形有关的角第一课时同步练习 题型:解答题
如图,将三角尺的直角顶点放在直线a上,a∥b,∠1=50°,∠2=60°,求∠3的度数.
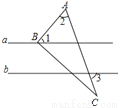
查看答案和解析>>
科目:初中数学 来源:数学人教版八年级上册第11章第二节与三角形有关的角第一课时同步练习 题型:单选题
一个三角形的一个内角等于另外两个内角的和,这个三角形是( )
A. 直角三角形 B. 锐角三角形 C. 钝角三角形 D. 何类三角形不能确定
A 【解析】【解析】 三角形的一个外角等于与它不相邻的两内角之和,又一个内角也等于另外两个内角的和,由此可知这个三角形中有一个内角和它相邻的外角是相等的,且外角与它相邻的内角互补,所以有一个内角一定是90°,故这个三角形是直角三角形.故选A.查看答案和解析>>
科目:初中数学 来源:人教版九年级上册数学 23.2.3关于原点对称的点的坐标 测试 题型:单选题
已知点P(2+m,n﹣3)与点Q(m,1+n)关于原点对称,则m﹣n的值是( )
A.1 B.﹣1 C.2 D.﹣2
D 【解析】 试题分析:根据关于原点对称的点的横坐标互为相反数,纵坐标互为相反数,可得m、n的值,根据有理数的减法,可得答案. 【解析】 由点P(2+m,n﹣3)与点Q(m,1+n)关于原点对称,得 2+m+m=0,n﹣3+1+n=0. 解得m=﹣1,n=1. m﹣n=﹣1﹣1=﹣2, 故选:D.查看答案和解析>>
科目:初中数学 来源:天津武清区数学试卷八年级《11.3 多边形及其内角和》同步测试 题型:解答题
如果一个凸多边形除了一个内角以外,其它内角的和为2570°,求这个没有计算在内的内角的度数.
130° 【解析】试题分析:设这个内角为x,根据多边形的内角和公式(n﹣2)•180°可知,多边形的内角度数是180°的倍数,然后利用数的整除性进行求解. 试题解析:【解析】 设这个多边形的边数是n,没有计算在内的内角的度数是x,则(n﹣2)•180°=2570°+x,n=16…50°,180°﹣50°=130°,∴这个多边形是17边形,没有计算在内的内角的度数为130°.查看答案和解析>>
科目:初中数学 来源:天津武清区数学试卷八年级《11.3 多边形及其内角和》同步测试 题型:填空题
五边形的内角和等于____度,十边形的对角线有__条.
540 35 【解析】【解析】 五边形的内角和=(5-2)×180°=540°,十边形的对角线条数=10×(10-3)÷2=35.故答案为:540;35.查看答案和解析>>
科目:初中数学 来源:山东省聊城市2018届九年级上学期期中考试数学试卷 题型:单选题
如图,一艘潜艇在海面下500米A处测得俯角为30°的海底C处有一黑匣子发出信号,继续在同一深度直线航行4000米后,在B处测得俯角为60°的海底也有该黑匣子发出的信号,则黑匣子所在位置点C在海面下的深度为( )
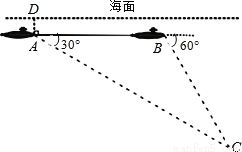
A. 2000米 B. 4000米 C. 2000米 D. (2000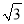 +500)米
+500)米
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com