练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如果一个凸多边形除了一个内角以外，其它内角的和为2570°，求这个没有计算在内的内角的度数．

    130° 【解析】试题分析：设这个内角为x，根据多边形的内角和公式（n﹣2）•180°可知，多边形的内角度数是180°的倍数，然后利用数的整除性进行求解． 试题解析：【解析】 设这个多边形的边数是n，没有计算在内的内角的度数是x，则（n﹣2）•180°=2570°+x，n=16…50°，180°﹣50°=130°，∴这个多边形是17边形，没有计算在内的内角的度数为130°．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：初一数学第一学期5.5应用一元一次方程-“希望工程”义演 同步练习 题型：填空题

    美术课外小组女同学占全组人数的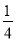，加入4个女同学后，女同学就占全组人数的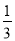，则美术课外小组原来的人数是____人．

    48

    查看答案和解析>>

    科目：初中数学 来源：数学人教版八年级上册第11章第二节与三角形有关的角第一课时同步练习 题型：填空题

    如图，将∠BAC沿DE向∠BAC内折叠，使AD与A′D重合，A′E与AE重合，若∠A=30°，则∠1+∠2=________．

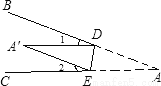
    60° 【解析】【解析】 根据题意得：∠A′=∠A=30°，在△ADE与△A′DE中，∠A+∠ADE+∠AED=180°，∠A′+∠A′DE+∠A′ED=180°，∴∠ADE+∠AED=150°，∠A′DE+∠A′ED=150°，∵（∠1+∠A′DE+∠ADE）+（∠AED+∠A′ED+∠2）=180°+180°=360°，∴∠1+∠2=60°．故答案为：60°．

    查看答案和解析>>

    科目：初中数学 来源：人教版九年级上册数学 23.2.3关于原点对称的点的坐标 测试 题型：填空题

    已知点A（﹣2m+4，3m﹣1）关于原点的对称点位于第四象限，则m的取值范围是 ．

    m＞2． 【解析】 试题分析：直接利用关于原点对称点的性质得出关于m的不等式进而求出答案． 【解析】 ∵点A（﹣2m+4，3m﹣1）关于原点的对称点位于第四象限， ∴﹣（﹣2m+4）＞0，﹣（3m﹣1）＜0， 解得：m＞2 则m的取值范围是：m＞2． 故答案为：m＞2．

    查看答案和解析>>

    科目：初中数学 来源：人教版九年级上册数学 23.2.3关于原点对称的点的坐标 测试 题型：单选题

    点P（2，﹣3）关于原点对称的点的坐标是（ ）

    A. （﹣2，﹣3） B. （2，3） C. （﹣2，3） D. （﹣3，2）

    C 【解析】试题分析：根据平面直角坐标系中任意一点P（x，y），关于原点的对称点是（﹣x，﹣y），即关于原点的对称点，横纵坐标都变成相反数． 【解析】 已知点P（2，﹣3）， 则点P关于原点对称的点的坐标是（﹣2，3）， 故选：C．

    查看答案和解析>>

    科目：初中数学 来源：天津武清区数学试卷八年级《11.3 多边形及其内角和》同步测试 题型：填空题

    已知：如图，求∠1＋∠2＋∠3＋∠4＋∠5＋∠6___________．

    360° 【解析】【解析】 如图，根据三角形中内角和为180°，有∠HGT=180°﹣（∠1+∠2），∠GHT=180°﹣（∠5+∠6），∠GTH=180°﹣（∠3+∠4），∴∠HGT+∠GHT+∠GTH=540°﹣（∠1+∠2+∠3+∠4+∠5+∠6），∵∠HGT+∠GHT+∠GTH=180°，∴180°=540°﹣（∠1+∠2+∠3+∠4+∠5+∠6），∴∠1+∠2+∠3+∠4+∠5+...

    查看答案和解析>>

    科目：初中数学 来源：天津武清区数学试卷八年级《11.3 多边形及其内角和》同步测试 题型：单选题

    一个多边形的边数增加，它的内角和也随着增加，而它的外角和( )．

    A. 随着增加 B. 随着减少 C. 保持不变 D. 无法确定

    C 【解析】【解析】 多边形的外角和等于360°，与边数无关．故选C．

    查看答案和解析>>

    科目：初中数学 来源：人教版九年级上册 22.3 二次函数的应用 同步测试 题型：解答题

    某超市销售樱桃，已知樱桃的进价为15元/千克，如果售价为20元/千克，那么每天可售出250千克，如果售价为25元/千克，那么每天可获利2000元，经调查发现：每天的销售量y（千克）与售价x（元/千克）之间存在一次函数关系．

    （1）求y与x之间的函数关系式；

    （2）若樱桃的售价不得高于28元/千克，请问售价定为多少时，该超市每天销售樱桃所获的利润最大？最大利润是多少元？

    （1）y=﹣10x+450；（2）售价为28元时，每天获利最大为2210元 【解析】试题分析：(1)、首先求出当x=25时的销售量，然后设函数解析式为：y=kx+b，将(20,250)和(25,200)代入求出函数解析式；(2)、设获利为W，然后根据总利润=单件利润×数量列出函数关系式，然后根据二次函数的性质求出最大值，得出答案． 试题解析：(1)、当x=25时，y=2000÷（25﹣...

    查看答案和解析>>

    科目：初中数学 来源：北师大版数学七年级上册5.3应用一元一次方程--水箱变高了课时练习（含解析） 题型：解答题

    在一次美化校园活动中，先安排31人去拔草，18人去植树，后又增派20人去支援他们，结果拔草的人数是植树的人数的2倍．问支援拔草和植树的分别有多少人？（只列出方程即可）

    31＋x＝2[18＋（20－x）]． 【解析】试题分析：设支援拔草的有x人，则支援植树的有（20-x）人，根据等量关系：原来拔草人数+支援拔草的人数=2×（原来植树的人数+支援植树的人数），列方程即可． 试题解析：设支援拔草的有x人，由题意得：31+x=2[18+（20-x）]．

    查看答案和解析>>

    同步练习册答案